Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 7 :
( bạn đạt A = (...) cái biểu thức đấy nhé, tự đặt )
Ta có :
\(\frac{1}{\sqrt{1}}=\frac{1}{1}>\frac{1}{10}=\frac{1}{\sqrt{100}}\)
\(\frac{1}{\sqrt{2}}>\frac{1}{\sqrt{100}}\)
\(\frac{1}{\sqrt{3}}>\frac{1}{\sqrt{100}}\)
\(............\)
\(\frac{1}{\sqrt{100}}=\frac{1}{\sqrt{100}}\)
\(\Rightarrow\)\(A=\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{100}}>\frac{1}{\sqrt{100}}+\frac{1}{\sqrt{100}}+\frac{1}{\sqrt{100}}+...+\frac{1}{\sqrt{100}}\)
\(A>\frac{100}{\sqrt{100}}=\frac{100}{10}=10\)
\(\Rightarrow\)\(A>10\)
Vậy \(A>10\)
Chúc bạn học tốt ~
Bạn làm được mình bài 7 thôi à, mình thấy bạn giỏi lắm mà. Mình có tới mấy chục bài cần giải cơ. Dạo này mình hỏi nhiều vì sắp đi thi.

a)Gọi tam giác: ABC có 3 đường cao :AH =BM =CN
SABC = 1/2 .BC.AH = 1/2 AC.BM =1/2 AB.CN
=> BC = AC = AB => Tam giác ABC đều
b) tam giác ABC đều => HA đông thời là trung tuyến
=> BH = 1/2 BC =1/2 AB
Áp dụng pi ta go cho tam giác ABH: AB2 = BH2 + AH2 => AB2 =AB2/4 + \(\left(\frac{\alpha\sqrt{3}}{2}\right)^2\)
3/4 AB2 = 3/4 \(\alpha\)2 =>AB2 =\(\alpha\)2 => AB =\(\alpha\)
Vậyđộ dàicạnh của tam giác đều là \(\alpha\)
Voi dien tich khong doi thi chieu cao va do dai day la 2 dai luong ti le nghich
=> tích của các chiều cao và độ dài các đây không đối = diện tích tam giác
Ma cac chieu cao bang nhau => cac canh bang nhau
=> tam giác đều
Diện tích của tam giác bằng nửa tích độ dài chiều cao và cạnh đáy ứng với nó và bằng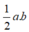 (
c
m
2
)
(
c
m
2
)
Chọn đáp án D