Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

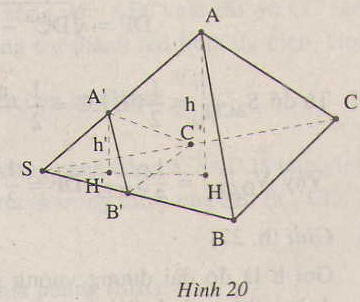
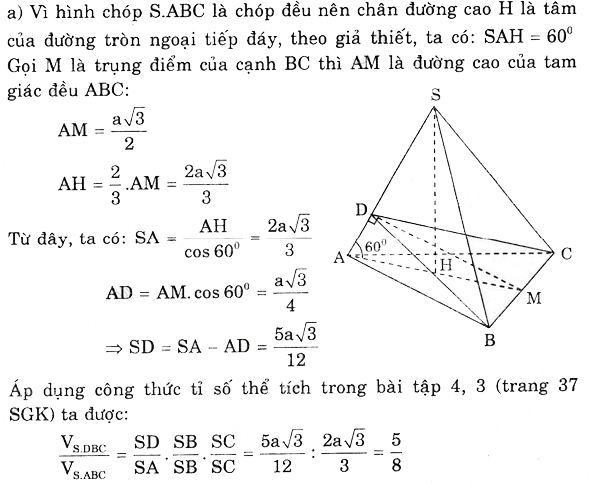
Gọi h và h’ lần lượt là chiều cao hạ từ A, A’ đến mặt phẳng (SBC).
Gọi S1 và S2 theo thứ tự là diện tích các tam giác SBC và SB’C’.
Khi đó ta có h′h=SA′SAh′h=SA′SA và 12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC
Suy ra VS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SCVS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SC
Đó là điều phải chứng minh.

S A B M N C
Dùng định lý hàm số Cosin tính được \(MN=2a\sqrt{3}\)
\(AM=2a\sqrt{2},AN=2a\). Tam giác vuông SAC có SC=2SA nên góc ASC =60 độ suy ra tam giác AMN vuông tại A.
Gọi H là trung điểm của MN, vì SA=SM=SN và tam giác AMN vuông tại A \(\Rightarrow SH\perp\left(AMN\right)\), tính được SH=a
Tính được \(V_{S.AMN}=\frac{2\sqrt{2}a^3}{3}\)
\(\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SM.SN}{SB.SC}=\frac{1}{3}\) \(\Rightarrow V_{S.ABC}=2\sqrt{2}a^3\)
Vậy d(C;(SAB)) =\(\frac{3V_{S.ABC}}{S_{\Delta SAB}}=\frac{6a^3\sqrt{2}}{3a^2}=2a\sqrt{2}\)

+)Gọi H là chân đường cao hạ từ A - -> BC
Tam giác AHC vuông tại H nên
AH = √(a² -a²/4) = a√3/2
Diện tích tam giác ABC là S(ABC) = 1/2.AH.BC= 1/2.a²√3/2
(dvdt)
+)Từ S hạ SK ┴ AH , Kết hợp AH ┴ BC ta có SK ┴ (ABC)
Hay SK là đường cao của hình chóp đều SABC
+) Bài cho góc giữa các mặt bên với đáy là 60 độ nên
góc giữa (SH,HK) = 60 độ
Tam giác vuông SKH có SK = HK.tan(60)
Tam giác vuông BKH có HK = a/2.tan(30) = a√3/6
- - > SK = a√3/6.tan(60) = a/2
Vậy V(SABC) =1/3.SK.S(ABC) = 1/3.a/2.1/2.a²√3/2
= a³√3/24 (dvtt)

Gọi V1 là thể tích của S.A'B'C'. Ta có:
\(\frac{V_1}{V}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}=\frac{1}{2}.\frac{1}{3}.\frac{1}{2}=\frac{1}{12}\)
=> \(\frac{V'}{V}=\frac{V-V_1}{V}=1-\frac{V_1}{V}=1-\frac{1}{12}=\frac{11}{12}\)
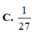
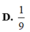
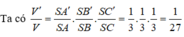
Chọn C.