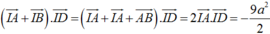Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ta có :
\(\Delta'=1^2-\left(-1-m\right)\left(m^2-1\right)=1-\left(-m^2+1-m^3+m\right)=1+m^2-1+m^3-m=m^3+m^2-m=m\left(m^2+m-1\right)\)để phương trình có nghiệm thì \(\Delta\ge0\)
hay \(m\left(m^2+m-1\right)\ge0\)
=> \(\left\{{}\begin{matrix}m\ge0\\m^2+m-1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}\ge0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2\ge\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left[{}\begin{matrix}m+\dfrac{1}{2}\ge\\m+\dfrac{1}{2}\le-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\dfrac{\sqrt{5}}{2}}\)

Bài 1a)
Áp dụng bất đẳng thức Cô-si cho từng cặp ta có
\(\left\{\begin{matrix}a+b\ge2\sqrt{ab}\\b+c\ge2\sqrt{bc}\\c+a\ge2\sqrt{ac}\end{matrix}\right.\)
\(=>\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ac}\)
\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\sqrt{\left(abc\right)^2}\)
\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8abc\) ( điều phải chứng minh )
Bài 1b)
Áp dụng bất đẳng thức Cô-si bộ 3 số cho từng cặp ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\a^2+b^2+c^2\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\left(abc\right)^2}\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9\sqrt[3]{\left(abc\right)^3}\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9abc\) (điều phải chứng minh )
Bài 1c) Ta có
\(\left(1+a\right)\left(1+b\right)\left(1+c\right)\ge\left(1+\sqrt[3]{abc}\right)^3\)
\(=>1+a+b\left(1+a\right)\left(1+c\right)\ge1^3+3.1^2.\sqrt[3]{abc}+3.1.\sqrt[3]{\left(abc\right)^2}+\sqrt[3]{\left(abc\right)^3}\)
\(=>\left(1+a+b+ab\right)\left(1+c\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>1+a+b+ab+c\left(1+a+b+ab\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>1+a+b+ab+c+ca+bc+abc\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>a+b+c+ab+bc+ca\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\)
Áp dụng bất đẳng thức Cô-si bộ 3 số cho vế trái ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\ab+bc+ac\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)
\(=>a+b+c+ab+bc+ac\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\) (điều phải chứng minh )
Bài 2a)
Áp dụng bất đẳng thức Cô-si cho từng cặp ta có
\(\left\{\begin{matrix}\frac{bc}{a}+\frac{ca}{b}\ge2\sqrt{\frac{bc}{a}.\frac{ca}{b}}=2\sqrt{c^2}=2c\\\frac{ca}{b}+\frac{ab}{c}\ge2\sqrt{\frac{ca}{b}.\frac{ab}{c}}=2\sqrt{a^2}=2a\\\frac{bc}{a}+\frac{ab}{c}\ge2\sqrt{\frac{bc}{a}.\frac{ab}{c}}=2\sqrt{b^2}=2b\end{matrix}\right.\)
\(=>2\left(\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\right)\ge2\left(a+b+c\right)\)
\(=>\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\ge a+b+c\) (điều phải chứng minh )
Bài 2b)
Chứng minh BĐT \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
Áp dụng BĐT Cô-si cho vế trái ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\end{matrix}\right.\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\frac{1}{abc}}\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9.\sqrt[3]{\frac{abc}{abc}}\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\) (điều phải chứng minh )
Ta có \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\ge\frac{3}{2}\)
\(=>\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}+3\ge\frac{3}{2}+3\)
\(=>\frac{a}{b+c}+1+\frac{b}{a+c}+1+\frac{c}{a+b}+1\ge\frac{9}{2}\)
\(=>\frac{a+b+c}{b+c}+\frac{a+b+c}{a+c}+\frac{a+b+c}{a+b}\ge\frac{9}{2}\)
\(=>\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge\frac{9}{2}\)
\(=>2\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9\)
Áp dụng BĐT vừa chứng minh \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
\(=>\left(b+c+a+c+a+b\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9 \) (Điều phải chứng minh )

ta thấy:\(\dfrac{a}{1+b^2}=a-\dfrac{ab^2}{1+b^2}\)
> áp dụng bđt cosi: 1+b2>=2b
>\(a-\dfrac{ab^2}{1+b^2}\ge a-\dfrac{ab^2}{2b}=a-\dfrac{ab}{2}\)
cminh tương tự với \(\dfrac{b}{1+c^2};\dfrac{c}{1+b^2}\)
cộng lần lượt 2 vế ta vừa cminh
>bthức tương đương với: a+b+c-\(\dfrac{ab+bc+ca}{2}\ge3-\dfrac{3}{2}=\dfrac{3}{2}\) đpcminh
(vì (a+b+c)2>=3(ab+bc+ca) hay 32>=3(ab+bc+ca)
> ab+bc+ca<=3)

Ta có : \(0< \alpha< \dfrac{\pi}{2}\)
=> \(\sin\alpha>0,\cos\alpha>\text{0},\tan\alpha>\text{0},\cot\alpha>\text{0}\)
a, Ta có : \(\sin\left(\alpha-\pi\right)=-\sin\left(\pi-\alpha\right)=-\left[-\sin\left(\alpha\right)\right]=\sin\alpha\)
=> \(sin\left(\alpha-\pi\right)>\text{0}\)
b, \(\cos\left(\dfrac{3\pi}{2}-\alpha\right)=\cos\left(\pi+\dfrac{\pi}{2}-\alpha\right)=-\cos\left(\dfrac{\pi}{2}-\alpha\right)=-sin\alpha\)
=> \(\cos\left(\dfrac{3\pi}{2}-\alpha\right)< \text{0}\)
c, \(tan\left(\alpha+\pi\right)=tan\alpha\)
=> \(tan\left(\alpha+\pi\right)>\text{0}\)
d, \(cot\left(\alpha+\dfrac{\pi}{2}\right)=-tan\alpha\)
=> \(cot\left(\alpha+\dfrac{\pi}{2}\right)< \text{0}\)



Chọn B.
Do I là trung điểm AD nên IA = ID = 3a/2
Ta có