Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

làm đc chưa bạn...
gọiE là tđ AD
suy ra NA = NH = NMNM
gọi F là tđ AM thì c/m đc KN KM KA KD bằng nhau
vậy AMN cân vuông tại N

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!

4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.

Giả sử C(c,3-c). Gọi I là giao điểm của AC và MN, suy ra \(\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AC}=\left(\dfrac{2(c+2)}{3};\dfrac{2(3-c)}{3}\right)\)
Do đó \(I\left(\dfrac{2c-2}{3};\dfrac{6-2c}{3}\right)\in MN:7x-6y-5=0\Rightarrow c=\dfrac{5}{2}\). Vậy \(C\left(\dfrac{5}{2};\dfrac{1}{2}\right)\)
Trung điểm của AC là \(P\left(\dfrac{1}{4};\dfrac{1}{4}\right),\overrightarrow{AC}\left(\dfrac{7}{2};\dfrac{1}{2}\right)\Rightarrow B\left(\dfrac{1}{4}+t;\dfrac{1}{4}-7t\right), D\left(\dfrac{1}{4}-t;\dfrac{1}{4}+7t\right)\).
Vì \(BP=CP=\dfrac{AC}{2}=\dfrac{5\sqrt{2}}{2}\)nên \(t=\pm\dfrac{1}{2}\)
Vậy \(B\left(\dfrac{3}{4};-\dfrac{13}{4}\right),D\left(-\dfrac{1}{4};\dfrac{15}{4}\right)\)hoặc \(B\left(-\dfrac{1}{4};\dfrac{15}{4}\right),D\left(\dfrac{3}{4};-\dfrac{13}{4}\right)\).

a) A=x^2+2
b) mình nghĩ x thuộc tập hợp R
c)GTNN của A=1/4 khi x=1/2

a: =>x+3>0
hay x>-3
b: \(\Leftrightarrow-\left(x-2\right)^2\left(x+2\right)>0\)
=>x+2<0
hay x<-2
c: =>x+4>0
hay x>-4
d: =>-3<x<4
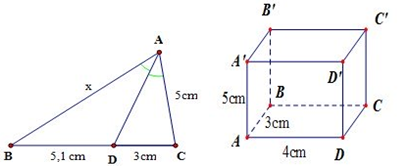
Đáp án A
Kẻ:
M H ⊥ A D ⇒ M H = A H = x 2 2 ⇒ H D = a − x 2 2
Tam giác HND có
H N 2 = D N 2 − 2 D N . H D . c o s 2 N D H ^
= a − x 2 2 2 + x 2 − 2 x a − x 2 2 = 5 2 x 2 − 2 2 a x + a 2
Vì:
M H ⊥ A D ⇒ M H / / A A ' ⇒ M H ⊥ A B C D ⇒ M H ⊥ H N
Tam giác MHN vuông tại H, có M N 2 = M H 2 + H N 2
= x 2 2 2 + 5 2 x 2 − 2 2 a x + a 2 = 3 x 2 − 2 2 a x + a 2 = 1 3 x − a 2 3 2 + a 2 3 ≥ a 2 3 ⇒ M N ≥ a 3 3 ⇒ M N min = a 3 3
Dấu “=” xảy ra khi x = a 2 3