Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Gọi \(I\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)
Tam giác \(A'BC\) cân tại \(A' \Rightarrow A'I \bot BC\)
\( \Rightarrow \left( {\left( {A'BC} \right),\left( {ABC} \right)} \right) = \left( {A'I,AI} \right) = \widehat {AI{\rm{A}}'} = {60^ \circ }\)
Tam giác \(ABC\) đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AA' = AI.\tan \widehat {AI{\rm{A}}'} = \frac{{3a}}{2}\)
b) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\)
\({V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{3{a^3}\sqrt 3 }}{8}\)

Đáp án A
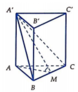
Gọi M là trung điểm BC. Ta có A ' M A ^ = 60 0
AM là trung tuyến trong tam giác đều cạnh a nên AM = a 3 2
![]()
![]()
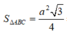
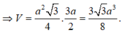

Đáp án D.
Gọi M là trung điểm BC, dựng ![]()
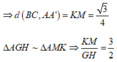
![]()
∆ AA'G vuông tại G, GH là đường cao => A'G = 1 3
Vậy 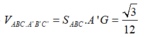

Đáp án A.
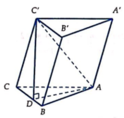
Theo giả thiết ta có CD' ⊥ (ABC). Áp dụng định lý Cô-sin cho ∆ ABD ta được:
AD = ![]()
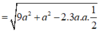
![]()
Hình chiếu vuông góc của AC’ trên mặt phẳng (ABC) là AD, vì vậy ta có góc giữa AC' và mặt phẳng (ABC) là góc C ' A D ^ = 45 0 => ∆ C'AD vuông cân tại D
![]()
Diện tích
∆
ABC là 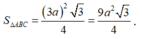
Do đó 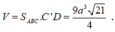

Đáp án C
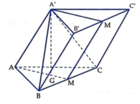
Ta dễ dàng chứng minh được AA'//(BCC'B')
![]()
![]()
Gọi G là trọng tâm của tam giác ABC. Suy ra A'G ⊥ (ABC)
Ta có
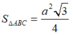
![]()
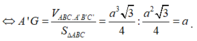
Lại có
![]()
![]()
Ta luôn có
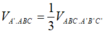
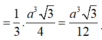
![]()
![]()

Gọi M, M' lần lượt là trung điểm của BC và B'C'. Ta có ![]() .
.![]()
Mà MM'//BB' nên BC ⊥ BB' => BCC'B' là hình chữ nhật
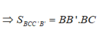
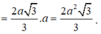
Từ:
![]()
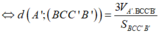
![]()
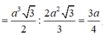
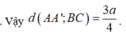
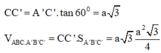
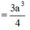



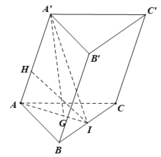

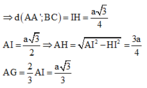
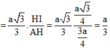

Đáp án A.
Gọi M là trung điểm của BC thì BC ⊥ (A'AM)
Từ A kẻ AH ⊥ A'M,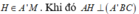
Suy ra
Góc giữa đường thẳng A'B và mặt phẳng (ABC) bằng góc A ' M A ^
Theo giả thiết ta có A ' M A ^ = 60 0
Đặt AB = 2x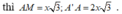
Từ giả thiết ta có
Do đó:
Vậy thể tích khối lăng trụ ABC.A'B'C' là V = 125 3 96 a 3
Phân tích phương án nhiễu.
Phương án B: Sai do HS tính đúng như trên nhưng nhớ nhầm công thức tính thể tích khối lăng trụ sang công thức tính thể tích khối chớp.
Cụ thể
Phương án C: Sai do HS giải như trên và tìm được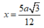 nhưng lại tính sai diện tích tam giác ABC. Cụ thể
nhưng lại tính sai diện tích tam giác ABC. Cụ thể
Do đó tính được
Phương án D: Sai do HS tính đúng như trên nhưng tính sai diện tích tam giác ABC. Cụ thể:
Do đó tính được V = 125 3 48 a 3