Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

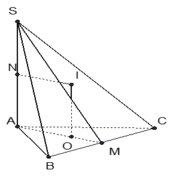
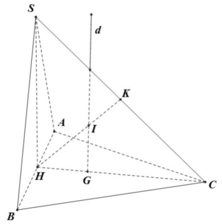
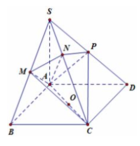
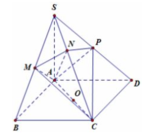
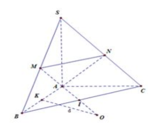
Gọi M là trung điểm SA và O là tâm đáy \(\Rightarrow AO=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\) ; \(AM=\dfrac{a}{2}\)
Qua O kẻ đường thẳng d song song SA, trong mặt phẳng (SAO) qua M kẻ đường thẳng song song AO cắt d tại I
\(\Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp
\(R=IA=\sqrt{IM^2+AM^2}=\sqrt{AO^2+AM^2}=\dfrac{a\sqrt{21}}{6}\)

Lời giải:
Ta có:
Vì $ABCD$ là hình vuông nên \(BC\perp AB\)
\(SA\perp (ABCD)\Rightarrow SA\perp BC\)
Từ hai điều trên suy ra \(BC\perp (SAB)\)
Do đó \(\angle (SC,(SAB))=\angle (SC,SB)=\angle CSB=30^0\)
\(\Rightarrow \frac{BC}{SB}=\tan 30=\frac{\sqrt{3}}{3}\Rightarrow SB=\sqrt{3}BC=\sqrt{3}a\)
Pitago: \(SA=\sqrt{SB^2-AB^2}=\sqrt{3a^2-a^2}=\sqrt{2}a\)
Do đó \(V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}\sqrt{2}a.a^2=\frac{\sqrt{2}}{3}a^3\)

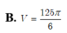


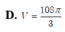

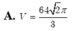
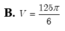
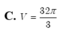
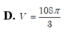



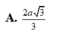
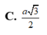

Đáp án C