K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
31 tháng 8 2018
Chọn C
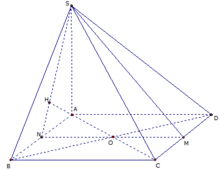
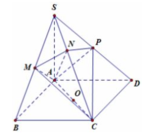
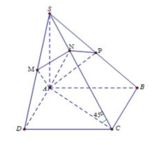
Gọi N là trung điểm của AB => BC // (SMN)
Suy ra d (BC, SM)=d (BC, (SMN))=d (B, (SMN))=d (A, (SMN)).
Dựng AH vuông góc với SN tại H
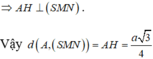
Lại có, trong tam giác vuông SAN:
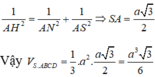
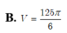


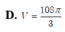
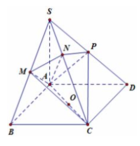

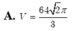
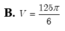
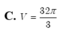
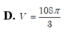

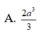
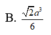







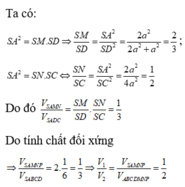

Lời giải:
Ta có:
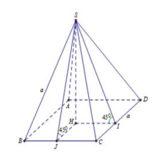
Vì $ABCD$ là hình vuông nên \(BC\perp AB\)
\(SA\perp (ABCD)\Rightarrow SA\perp BC\)
Từ hai điều trên suy ra \(BC\perp (SAB)\)
Do đó \(\angle (SC,(SAB))=\angle (SC,SB)=\angle CSB=30^0\)
\(\Rightarrow \frac{BC}{SB}=\tan 30=\frac{\sqrt{3}}{3}\Rightarrow SB=\sqrt{3}BC=\sqrt{3}a\)
Pitago: \(SA=\sqrt{SB^2-AB^2}=\sqrt{3a^2-a^2}=\sqrt{2}a\)
Do đó \(V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}\sqrt{2}a.a^2=\frac{\sqrt{2}}{3}a^3\)