Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M N P Q
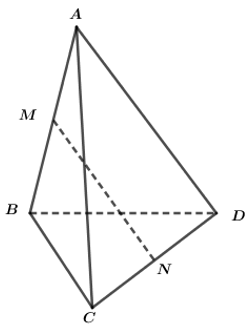
a/ Trong mp (BCD) dựng đường thẳng // với CD cắt BD tại P => CD//NP (1)
=> mp (MNP) là mp \(\alpha\)
Trong mp (ACD) từ M dựng đường thẳng //CD cắt AC tại Q => CD//MQ (2)
Từ (1) và (2) => NP//MQ => MPNQ là thiết diện của tứ diện ABCD với mp \(\alpha\)
b/
Xét tg ACD có
MQ//CD và MA=MD => QA=QC (trong tam giác đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại của tam giác => MQ là đường trung bình của tg ACD \(\Rightarrow MQ=\frac{CD}{2}\)
Ta có MQ//NP để MPNQ là hình bình hành thì \(MQ=NP=\frac{CD}{2}\) (tứ giác có 1 cặp cạnh đối // và = nhau thì tứ giác là hbh)
=> NP là đường trung bình của tg BCD => N là trung điểm của BC

Toán THPT lớp 10, 11, 12 : Em vào h.vn để được các bạn giúp đỡ nhé!

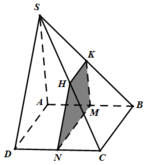

=> giao tuyến của (SCD) và (α) là NH// SD.
+ lại có HK là giao tuyến của (α) và (SBC) .
Thiết diện là tứ giác MNHK.
Ba mặt phẳng (ABCD) ; (SBC) và (α) đôi một cắt nhau theo các giao tuyến là MN; HK và BC mà MN// BC nên MN// HK. Vậy thiết diện là một hình thang .
Chọn B.


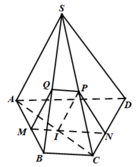







+ Ta tìm thiết diện của hình chóp cắt bởi (α):
Trong ( SAB) dựng MQ // SA( Q thuộc SB)
Gọi I là giao điểm của AC và MN.
Trong mp ( SAC); dựng IP// SA với P thuộc SC.
Khi dó thiết diện cần tìm là tứ giác MNPQ.
+ Tứ giác MNPQ là một hình thang khi MN// PQ hoặc MQ// PN.
=> MN//PQ nên tứ giác MNPQ là hình thang.
Vậy để tứ giác MNPQ là hình thang thì điều kiện là MN//BC.
Chọn C