PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 4 2017
Hướng dẫn:
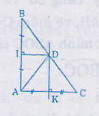
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800
19 tháng 4 2017
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800
28 tháng 2 2018
B A E M K C H
a) Bạn ghi câu a) không rõ ràng nên mình thay thế bằng ý kiến của mình nhé !
CMR : \(\Delta ABE=\Delta HBE\)
Xét \(\Delta ABE,\Delta HBE\) có :
\(BA=BH\left(gt\right)\)
\(\widehat{ABE}=\widehat{HBE}\) (BE là tia phân giác của \(\widehat{B}\) )
\(BE:chung\)
=> \(\Delta ABE=\Delta HBE\left(c.g.c\right)\)
b) Gọi \(AH\cap BE=\left\{O\right\};O\in BE\)
Xét \(\Delta ABO,\Delta HBO\) có :
\(AB=BH\left(gt\right)\)
\(\widehat{ABO}=\widehat{HBO}\) (BE là tia phân giác của \(\widehat{B}\) ; \(O\in BE\))
AO : Chung
=> \(\Delta ABO=\Delta HBO\left(c.g.c\right)\)
=> \(\widehat{BOA}=\widehat{BOH}\) (2 góc tương ứng)
Mà : \(\widehat{BOA}+\widehat{BOH}=180^o\left(Kềbù\right)\)
=> \(\widehat{BOA}=\widehat{BOH}=\dfrac{180^o}{2}=90^o\)
=> \(BO\perp AH\)
Hay : \(BE\perp AH\)
c) Ta chứng minh được : \(\Delta BKE=\Delta BCE\)
Suy ra : \(EK=EC\) (2 cạnh tương ứng)
d) Xét \(\Delta ABC\) có :
BE là tia phân giác của \(\widehat{ABC}\) (1)
Xét \(\Delta KEM,\Delta CEM\) có :
\(EK=EC\left(cmt\right)\)
\(EM:chung\)
\(KM=CM\) (M là trung điểm của KC)
=> \(\Delta KEM=\Delta CEM\left(c.c.c\right)\)
=> \(\widehat{MEK}=\widehat{MEC}\) (2 góc tương ứng)
=> EM là tia phân giác của \(\widehat{KEC}\) (2)
Từ (1) và (2) => \(BE\equiv ME\)
=> B, E, M thẳng hàng
=> đpcm.
23 tháng 12 2016
a) xét tam giác oam và tam giác obm có:
OA = OB ( GT )
AM = MB ( GT )
OM chung
=> tam giác oam = tam giác obm ( c.c.c)
b) ta có oam= obm( theo a )
=> oam = obm (2 góc t.ư)
=> oam+ obm= 180°(2 góc kề bù)
=> oam= obm = 180° : 2 = 90°
=> om vuông góc ab
c) xét tam giác amd và tam giác bmd có
am= bm(gt)
da=db(gt)
md chung
=> tam giác amd= tam giác bmd(c.c.c)
=> dam= dbm( 2 góc t.ư)
=> dam+dbm=180° (2góc kề bù)
=> dam= dbm= 180° : 2 = 90°
=> md vuông góc ab
Mà om vuông góc ab ( theo b )
md vuông góc ab(cmt)
Mà M thuộc od => M,O,D thẳng hàng
Bn tự vẽ hình hộ mk nhé!
4 tháng 5 2019
Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
4 tháng 5 2019
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau
25 tháng 12 2018
???????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
25 tháng 12 2018
a, xét tam giác aec và tam giác aed có
ae chung
ec=ed(gt)
ac=ad(gt)
=>tam giác aec = tam giác aed(ccc)
b. từ cma ta có tam giác aec = tam giác aed
=>góc cae=góc dac(2 góc tg ứng)
xét tam giác cai và tam giác dai có
ca=da(gt)
góc cae=góc dac(cmt)
ai chung
=>tam giác cai =tam giác dai(cgc)
=>ci=di(2 cạnh tg ứng)
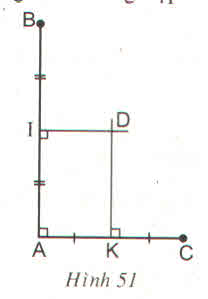
Hình 51
Từ hình vẽ ta có:
+ DK là đường trung trực của AC ⇒ DA = DC.
+ DI là đường trung trực của AB ⇒ DA = DB.
+ Ta có : DI // AC (vì cùng ⏊ AB)
Mà DK ⏊ AC ⇒ DK ⏊ DI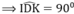
+ Xét ∆ADK và ∆CDK có:
AD = DC
AK = CK (gt)
DK chung
⇒ ∆ADK = ∆CDK (c.c.c)
+ Xét ∆ADI và ∆BDI có :
AD = BD
AI = BI (gt)
DI chung
⇒ ∆ADI = ∆BDI (c.c.c)
Từ (1) và (2) suy ra
Vậy B, D, C thẳng hàng.