Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(y'=3x^2-6x+m^2\Rightarrow y'=0\Leftrightarrow3x^2-6x+m^2=0\left(1\right)\)
Hàm số có cực trị \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt \(x_1;x_2\)
\(\Leftrightarrow\Delta'=3\left(3-m^2\right)>0\Leftrightarrow-\sqrt{3}< m< \sqrt{3}\)
Phương trình đường thẳng d' đi qua các điểm cực trị là : \(y=\left(\frac{2}{3}m^2-2\right)x+\frac{1}{3}m^2\)
=> Các điểm cực trị là :
\(A\left(x_1;\left(\frac{2}{3}m^2-2\right)x_1+\frac{1}{3}m^2+3m\right);B\left(x_2;\left(\frac{2}{3}m^2-2\right)x_2+\frac{1}{3}m^2+3m\right);\)
Gọi I là giao điểm của hai đường thẳng d và d' :
\(\Rightarrow I\left(\frac{2m^2+6m+15}{15-4m^2};\frac{11m^2+3m-30}{15-4m^2}\right)\)
A và B đối xứng đi qua d thì trước hết \(d\perp d'\Leftrightarrow\frac{2}{3}m^2-2=-2\Leftrightarrow m=0\)
Khi đó \(I\left(1;-2\right);A\left(x_1;-2x_1\right);B\left(x_2;-2x_2\right)\Rightarrow I\) là trung điểm của AB=> A và B đối xứng nhau qua d
Vậy m = 0 là giá trị cần tìm

Ta có : \(y'=3x^2-6mx+3\left(m^2-1\right)\)
Để hàm số có cực trị thì phương trình \(y'=0\) có 2 nghiệm phân biệt
\(\Leftrightarrow x^2-2mx+m^2-1=0\) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta=1>0\) với mọi m
Cực đại của đồ thị hàm số là A(m-1;2-2m) và cực tiểu của đồ thị hàm số là B (m+1; -2-2m)
Theo giả thiết ta có :
\(OA=\sqrt{2}OB\Leftrightarrow m^2+6m+1\Leftrightarrow\begin{cases}m=-3+2\sqrt{2}\\m=-3-2\sqrt{2}\end{cases}\)
Vậy có 2 giá trị m là \(\begin{cases}m=-3+2\sqrt{2}\\m=-3-2\sqrt{2}\end{cases}\)

a) Ta có : \(y'=3x^2+2\left(m-1\right)x+m\left(m-3\right)\)
Hàm số (1) có cực đại và cực tiểu nằm 2 phía đối với trục tung <=> phương trình : \(3x^2+2\left(m-1\right)x+m\left(m-3\right)=0\) có 2 nghiệm phân biệt trái dấu
\(\Leftrightarrow P< 0\Leftrightarrow m\left(m-3\right)< 0\Leftrightarrow0< m< 3\)
Vậy \(0< m< 3\) là giá trị cần tìm
b) Khi m = 1 ta có : \(y=x^3-2x\).
Gọi \(M\left(a;a^3-2a\right)\in\left(C\right),a\ne0\)
Ta có \(y'=3x^2-2\) nên hệ số góc của \(\Delta\) là \(y'\left(a\right)=3a^2-2\)
Ta có \(\overrightarrow{OM}\left(a;a^3-2a\right)\) nên hệ số góc đường thẳng OM là \(k=a^2-2\)
Do đó : \(\Delta\perp OM\Leftrightarrow y'_a.k=-1\)
\(\Leftrightarrow\left(3a^2-2\right)\left(a^2-2\right)=-1\Leftrightarrow3a^4-8a^2+5=0\)
\(M_1\left(1;-1\right);M_1\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a^2=1\\a^2=\frac{5}{3}\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a=\pm1\\a=\pm\frac{\sqrt{5}}{3}\end{array}\right.\)(Thỏa mãn)
Suy ra có 4 điểm thỏa mãn đề bài :\(M_1\left(1;-1\right);M_2\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\)

\(\Leftrightarrow y'=0\)
có 2 nghiệm phân biệt \(x_1,x_2\) thỏa mãn \(x_1\)<\(x_2\)<1
\(\Leftrightarrow\)\(\begin{cases}\Delta'=4m^2-m-5>0\\f\left(1\right)=-5m+7>0\\\frac{S}{2}=\frac{2m-1}{3}<1\end{cases}\)\(\Leftrightarrow\)\(\frac{5}{4}\)<m<\(\frac{7}{5}\)

Câu 2:
$y'=-3x^2+6x+(m-2)=0$
Để hàm số có 2 điểm cực trị $x_1,x_2$ đồng nghĩa với PT $-3x^2+6x+(m-2)=0$ có 2 nghiệm phân biệt $x_1,x_2$
$\Leftrightarrow \Delta'=9+3(m-2)>0\Leftrightarrow m>-1(1)$
Hai điểm cực trị cùng dương khi:
\(\left\{\begin{matrix} x_1+x_2=2>0\\ x_1x_2=\frac{m-2}{-3}>0\end{matrix}\right.\Leftrightarrow m< 2(2)\)
Từ $(1);(2)\Rightarrow -1< m< 2$
Đáp án C.
Câu 2:
Để đths có 2 điểm cực trị thì trước tiên:
$y'=x^2-2mx+m^2-4=0$ có 2 nghiệm phân biệt $x_1,x_2$
Điều này xảy ra khi $\Delta'=m^2-(m^2-4)>0\Leftrightarrow m\in\mathbb{R}$
Để 2 điểm cực trị của đồ thị $y$ nằm về hai phía của trục tung thì: $x_1x_2< 0$
$\Leftrightarrow m^2-4< 0$
$\Leftrightarrow -2< m< 2$
Đáp án A.

lưa ý pt \(x^2=m^2-m+1\)có nghiệm với x phải #0 vì nếu = 0 thì trùng => sai
nhưng nghiệm \(\left(+,-\right)\sqrt{m^2-m+1}\)luôn #0 rồi khỏi lo
\(y'=6x^2-6\left(m+1\right)x+6m\)
ta có y/y'=\(\left(3m-1\right)x+m^3+m^2+m\)
suy ra y= \(\left(3m-1\right)x+m^3+m^2+m\)là pt của dường thẳng đi qua A và B
de-ta \(=9\left(m+1\right)^2-36m\)
y' có 2 \(n_o\)phân biệt khi m#1
hai hoành độ của hai điểm cực trị là :
\(X=\dfrac{-b\left(+,-\right)\sqrt{deta}}{a}=\)
\(\left[{}\begin{matrix}\dfrac{m+3}{2}\\\dfrac{3m-1}{2}\end{matrix}\right.\)<=>y=\(\left[{}\begin{matrix}2m^3+5m^2+10m+3\\2m^3+11m^2+4m+1\end{matrix}\right.\)(tìm y bằng cách thế x vào pt đường thẳng )
khoảng cách giữa hai điểm AB =\(\sqrt{2}\)
ta có pt : \(2=\left(\dfrac{m+3}{2}-\dfrac{3m-1}{2}\right)^2+\left(2m^3+5m^2+10m-3-\left(2m^3+11m^2-4m+1\right)\right)^2\)
lại sai chỗ nào rồi 0 ra nghiệm , cậu tính lại thử , cách giả là như vậy

Ta có \(y'=3x^2-3\left(m-2\right)x-3\left(m-1\right)\), với mọi \(x\in R\)
\(y'=0\Leftrightarrow x^2-\left(m-2\right)x-m+1=0\Leftrightarrow x_1=-1;x_2=m-1\)
Chú ý rằng với m > 0 thì \(x_1< x_2\). Khi đó hàm số đạt cực đại tại \(x_1=-1\) và đạt cực tiểu tại \(x_2=m-1\). Do đó :
\(y_{CD}=y\left(-1\right)=\frac{3m}{2};y_{CT}=y\left(m-1\right)=-\frac{1}{2}\left(m+2\right)\left(m-1\right)^2+1\)
Từ giả thiết ta có \(2.\frac{3m}{2}-\frac{1}{2}\left(m+2\right)\left(m-1\right)^2+1\Leftrightarrow6m-6-\left(m+2\right)\left(m-1\right)^2=0\)
\(\Leftrightarrow\left(m-1\right)\left(m^2+m-8\right)=0\Leftrightarrow m=1;m=\frac{-1\pm\sqrt{33}}{2}\)
Đối chiếu yêu cầu m > 0, ta có giá trị cần tìm là \(m=1;m=\frac{-1\pm\sqrt{33}}{2}\)

Bài 1: Ta có
\(y'=0\Leftrightarrow x[2mx^2-(m+1)]=0\)
\(\Leftrightarrow \left[\begin{matrix} x=0\\ 2mx^2-(m+1)=0(1)\end{matrix}\right.\)
Một điểm nằm trên trục tọa độ thì tung độ hoặc hoành độ phải bằng $0$. Do đó yêu cầu đề bài được đáp ứng khi $y'=0$ có nghiệm $x=0$ hoặc nếu $x$ khác $0$ thì tung độ tương ứng phải bằng $0$
+) Nếu \(m=0\) : $(1)$ vô nghiệm . $y'=0$ có nghiệm duy nhất $x=0$ (thỏa mãn)
+) Nếu $m=-1$ : $(1)$ có nghiệm $x=0$ (thỏa mãn)
+) Nếu $-1< m< 0$. Từ \((1)\Rightarrow x^2=\frac{m+1}{2m}< 0\) (vô lý) nên $(1)$ vô nghiệm. $y'=0$ có nghiệm duy nhất $x=0$ (thỏa mãn)
+) Nếu \(m>0\) hoặc \(m< -1\)
$(1)$ có 2 nghiệm \(x=\pm \sqrt{\frac{m+1}{2m}}\neq 0\)
\(\Rightarrow y=m(\pm \sqrt{\frac{m+1}{2m}})^4-(m+1)(\pm \sqrt{\frac{m+1}{2m}})^2+(m+1)\)
\(=\frac{(m+1)^2}{4m}-\frac{(m+1)^2}{2m}+(m+1)\)
\(=(m+1)-\frac{(m+1)^2}{4m}=0\)
\(\Leftrightarrow \left[\begin{matrix} m=-1\\ m=\frac{1}{3}\end{matrix}\right.\) . Vì \(\Rightarrow m=\frac{1}{3}\)
Vậy \(-1\leq m\leq 1 \text{or m}=\frac{1}{3}\)
Bài 2:
Ta có: \(y'=4x^3+4mx=0\Leftrightarrow x(x^2+m)=0\)
Nếu $m\geq 0$. PT $y'=0$ có duy nhất nghiệm $x=0$. Ta chỉ thu được 1 điểm cực trị (loại)
Nếu $m<0$. Ngoài $x=0$ pt $y'=0$ còn có 2 nghiệm \(x=\pm \sqrt{-m}\neq 0\)
(thu được 3 cực trị)
Khi đó:
\(y=(\pm \sqrt{-m})^4+2m(\pm \sqrt{-m})^2+4=m^2-2m^2+4=4-m^2\)
Để điểm cực trị nằm trên trục tọa độ thì \(y=0\Leftrightarrow 4-m^2=0\Leftrightarrow m=-2\) (do $m< 0$)
Vậy \(m=-2\)
Ta có
Suy ra đồ thị có hai điểm cực tiểu là A - m 2 - m + 1 ; y C T và B m 2 - m + 1 ; y C T
Khi đó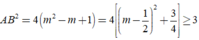
Dấu xảy ra khi m=1/2.
Chọn B.