Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
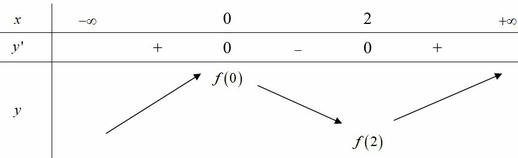
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.

Từ \(f\left(x\right)+f\left(\frac{1}{x}\right)=x^2\); lần lượt thay \(x=2\) và \(x=\frac{1}{2}\) vào, ta có:
\(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\) và \(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\Leftrightarrow3f\left(2\right)+f\left(\frac{1}{2}\right)=\frac{1}{4}\)
Giải hệ phương trình với 2 ẩn \(f\left(2\right)\) và \(f\left(\frac{1}{2}\right)\)
Tìm được \(f\left(2\right)=\frac{-13}{32}\)
Ta có \(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\) (1)
Thay \(x\rightarrow\frac{1}{x}\) được \(f\left(\frac{1}{x}\right)+3f\left(x\right)=\frac{1}{x^2}\)
\(\Leftrightarrow3f\left(\frac{1}{x}\right)+9f\left(x\right)=\frac{3}{x^2}\) (2)
Lấy (2) trừ (1) theo vế : \(8f\left(x\right)=\frac{3}{x^2}-x^2\)
\(\Leftrightarrow f\left(x\right)=\frac{1}{8}\left(\frac{3}{x^2}-x^2\right)\)
Vậy f(2) = -13/32

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm
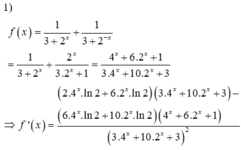
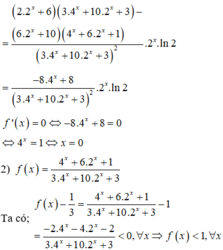
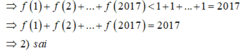
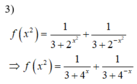

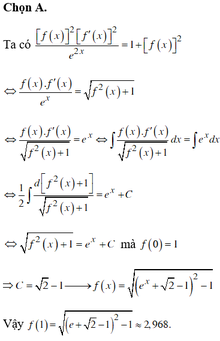





1 ) f ( x ) = 1 3 + 2 x + 1 3 + 2 x = 1 3 + 2 x + 2 x 3 . 2 x + 1 = 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3
⇒ f ' ( x ) = 2 . 4 x . ln 2 + 5 . 2 x . ln 2 3 . 4 x + 10 . 2 x + 3 3 . 4 x + 10 . 2 x + 3 2
- 6 . 4 x . ln 2 + 10 . 2 x . ln 2 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3 2
= 2 . 2 x + 6 3 . 4 x + 10 . 2 x + 3 - 6 . 2 x + 10 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3 2 . 2 x . ln 2 = - 8 . 4 x + 8 3 . 4 x + 10 . 2 x + 3 2 . 2 x . ln 2
f ' ( x ) = 0 ⇔ - 8 . 4 x + 8 = 0 ⇔ 4 x = 1 ⇔ x = 0
2 ) f ( x ) = 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3
Ta có
f ( x ) - 1 3 = 4 x + 6 . 2 x + 1 3 . 4 x + 10 . 2 x + 3 - 1 = - 2 . 4 x - 4 . 2 x - 2 3 . 4 x + 10 . 2 x + 3 < 0 , ∀ x ⇒ f ( 1 ) + f ( 2 ) + . . + f ( 2017 ) < 1 + 1 + . . . + 1 = 2017 ⇒ f ( 1 ) + f ( 2 ) + . . + f ( 2017 = 2017 ⇒ 2 ) s a i
3) f ( x 2 ) = 1 3 + 2 x + 1 3 + 2 - x ⇒ f ( x 2 ) = 1 3 + 4 x + 1 3 + 4 - x l à s a i
Chọn đáp án A.