Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔABC và ΔEFD
Để ΔABC=ΔEFD theo trường hợp c-g-c thì BC=FD
b: ΔABC=ΔEFD
nên AB=EF=5cm; AC=ED=6cm; BC=FD=6cm
=>\(C_{ABC}=C_{EFD}=5+6+6=17\left(cm\right)\)

ΔABC=ΔDEIΔABC=ΔDEI
⇒AB=DE=5(cm)⇒AB=DE=5(cm) ( 2 cạnh tương ứng )
⇒BC=EI=8(cm)⇒BC=EI=8(cm) ( 2 cạnh tương ứng )
⇒AC=DI=6(cm)⇒AC=DI=6(cm) ( 2 cạnh tương ứng )
Chu vi của ΔABCΔABC là:
AB+BC+CA=5+8+6=19(cm)AB+BC+CA=5+8+6=19(cm)
Chu vi của ΔDEIΔDEI là:
DE+EI+DI=5+8+6=19(cm)DE+EI+DI=5+8+6=19(cm)
Vậy........
ΔABC=ΔDEf
⇒AB=DE=5(cm) ( 2 cạnh tương ứng )
⇒BC=EI=8(cm) ( 2 cạnh tương ứng )
⇒AC=DI=6(cm) ( 2 cạnh tương ứng )
Chu vi của ΔABCΔABC là:
AB+BC+CA=5+8+6=19(cm)
Chu vi của ΔDEIΔDEI là:
DE+EI+DI=5+8+6=19(cm)
Vậy........

Vì \(\Delta ABC=\Delta DEF\)
nên AB = DE = 4cm;
BC = EF = 6cm;
AC = DF = 5cm
Khi đó: \(P_{\Delta ABC}=P_{\Delta DEF}=4+5+6=15\left(cm\right)\)
Vậy \(P_{\Delta ABC}=P_{\Delta DEF}=15cm.\)

1/ Ta có: tam giác ABC = tam giác DEF
=> góc A = góc D
góc B = góc E
góc C = góc F
Ta có: góc A + góc B + góc C = 1800
1300 + góc C = 1800
góc C = 1800-1300 = 500
Ta có: góc A + góc B = 1300
góc A + 550 = 1300
góc A = 1300 - 550 =750
Vậy góc A = góc D = 750
góc B = góc E = 550
góc C = góc F = 500
2/ Ta có: tam giác DEF = tam giác MNP
=> DE = MN
EF = NP
FD = PM
Ta có: EF + FD = 10 cm
Mà NP - MP = EF - FD = 2 cm
EF = (10 + 2) : 2 = 6 (cm)
FD = (10 - 2) : 2 = 4 (cm)
Vậy DE = MN = 3 cm
EF = NP = 6 cm
FD = MP = 4 cm
1) Ta có: ( \(\widehat{A}\) + \(\widehat{B}\)) + \(\widehat{C}\) = 180o
hay 130o + \(\widehat{C}\) = 180o
\(\Rightarrow\) \(\widehat{C}\) = 180o - 130o = 50o
Vì ΔABC = ΔDEF nên ta có:
\(\widehat{C}\) = \(\widehat{F}\) = 50o
\(\widehat{E}\) = \(\widehat{B}\) = 55o
Ta có: \(\widehat{A}\) + \(\widehat{B}\) = 130o hay \(\widehat{A}\) + 55o = 130o
\(\Rightarrow\) \(\widehat{A}\) = 130o - 55o = 75o
\(\Leftrightarrow\) \(\widehat{A}\) = \(\widehat{D}\) = 75o
Vậy: \(\widehat{A}\) = \(\widehat{D}\) = 75o
\(\widehat{B}\) = \(\widehat{E}\) = 55o
\(\widehat{C}\) = \(\widehat{F}\) = 50o
2) ΔDEF = ΔMNP nên:
\(\Rightarrow\) DE = MN
EF = NP
FD = PM
Ta có: EF + FD = 10cm
mà ΔDEF = ΔMNP
\(\Rightarrow\) NP - MP = EF - FD = 2cm
\(\Rightarrow\) EF = \(\frac{10+2}{2}\) = 6cm
FD = 6cm - 2cm = 4cm
Vậy: DE= MN = 3cm
EF = NP = 6cm
FD = PM = 4cm
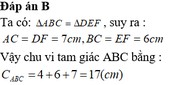
Ta có:
ΔABC=ΔDEF\(\Rightarrow\left\{{}\begin{matrix}AB=DE\\BC=EF\\AC=DF\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}AB+DE=10\left(cm\right)\\EF=6\left(cm\right)\\AC=7\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{10}{2}=5\left(cm\right)\\BC=6\left(cm\right)\\AC=7\left(cm\right)\end{matrix}\right.\)
Chu vi ΔABC là:
\(C_{ABC}=AB+BC+AC=5+6+7=18\left(cm\right)\)