

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

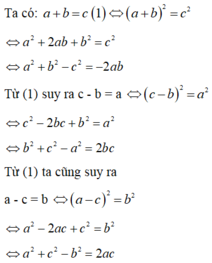


Do \(a+b+c=0\)
\(\Rightarrow c=-a-b\)
\(\Rightarrow c^2=a^2+2ab+b^2\)
Tương tự,ta có:
\(a^2=b^2+2bc+c^2\)
\(b^2=a^2+2ac+c^2\)
Thay vào bài toán,ta được:
\(P=\frac{c^2}{a^2+b^2-\left(a^2+2ab+b^2\right)}+\frac{a^2}{b^2+c^2-\left(b^2+2bc+c^2\right)}+\frac{b^2}{c^2+a^2-\left(a^2+2ac+c^2\right)}\)
\(P=\frac{-c^2}{2ab}+\frac{-a^2}{2bc}+\frac{-b^2}{2ac}\)
\(P=\frac{-\left(a^3+b^3+c^3\right)}{2abc}\)
Do \(a+b+c=0\Rightarrow-a=b+c\)
\(\Rightarrow-a^3=b^3+c^3+3bc\left(b+c\right)\)
\(\Rightarrow-a^3=b^3+c^3-3abc\)
\(\Rightarrow a^3+b^3+c^3=3abc\)
Khi đó,ta có:
\(P=\frac{-\left(3abc\right)}{2abc}=-\frac{3}{2}\)

Ta có:\(a+b+c=0\Rightarrow a+b=-c\Rightarrow\left(a+b\right)^2=\left(-c\right)^2\)
\(\Rightarrow a^2+b^2+2ab=c^2\Rightarrow a^2+b^2-c^2=-2ab\)
Tươmg tự ta cũng có:\(b^2+c^2-a^2=-2bc\) và \(c^2+a^2-b^2=-2ca\)
\(\Rightarrow P=\frac{1}{-2ab}+\frac{1}{-2bc}+\frac{1}{-2ca}=-\frac{1}{2}\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\right)=-\frac{1}{2}\left(\frac{a+b+c}{abc}\right)=0\)
a+b+c=0 => a= -(b+c) TƯƠNG TỰ
b= -(a+c) ; c= -(b+a)
ta co P= \(\frac{1}{\left(b+c\right)^2+\left(b^2-c^2\right)}+\frac{1}{\left(a+c\right)^2+\left(a^2-c^2\right)}+\frac{1}{\left(b+a\right)^2+\left(b^2-a^2\right)}\)
=> P= \(\frac{1}{2c\left(b+c\right)}+\frac{1}{2b\left(a+c\right)}+\frac{1}{2a\left(b+c\right)}\)
thay b+c=-a; a+c=-b ; a+b=-c (như trên )
=> P= \(\frac{1}{-2ac}+\frac{1}{-2ab}+\frac{1}{-2bc}\)
QUY ĐONG CAC MAU THUC TA CO
P= \(\frac{a+b+c}{-2abc}\)
a+b+c=0 => P=0

\(a+b+c=0\Leftrightarrow a+b=-c\Leftrightarrow\left(a+b\right)^2=\left(-c\right)^2\Leftrightarrow a^2+b^2+2ab=c^2\Leftrightarrow a^2+b^2-c^2=-2ab\)
tương tự ta có: b2+c2-a2=-2bc ; a2+c2-b2=-2ac
Do đó \(P=\frac{1}{-2bc}+\frac{1}{-2ca}+\frac{1}{-2ab}=\frac{a+b+c}{-2abc}=0\)

http://diendantoanhoc.net/topic/152549-t%C3%ADnh-fraca2a2-b2-c2-fracb2b2-c2-a2fracc2c2-b2-a2/
Ta có: \(a+b+c=0\)
\(\Rightarrow1\hept{\begin{cases}a+b=-c\\b+c=-a\\c+a=-b\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a^2+b^2=-2ab+c^2\\b^2+c^2=-2bc+a^2\\c^2+a^2=-2ac+b^2\end{cases}}\)
\(\Rightarrow1A=\frac{a^2}{a^2+2bc-a^2}+\frac{b^2}{b^2+2ac-b^2}+\frac{c^2}{c^2+2ab-c^2}\)
\(=\frac{a^3+b^3+c^3}{2abc}=\frac{a^3+b^3+c^3-3abc+3abc}{2abc}\)
\(=\frac{\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)+3abc}{2abc}\)
\(=\frac{3}{2}\)

Ta có: a + b + c = 0
=> ( a + b + c )2 = 0
=> a2 + b2 + c2 + 2ab +2ac+ 2bc = 0
=> 2 + 2( ab + ac + bc ) = 0
=> 2( ab + ac +bc ) = - 2
=> ab + ac + bc = -1
=> ( ab + ac + bc )2 = 1
=> a2b2 + a2c2 + b2c2 + 2a2bc + 2ab2c + 2abc2 = 1
=> a2b2 + a2c2 + b2c2 + 2abc( a + b + c ) = 1
=> a2b2 + a2c2 + b2c2 + 2abc x 0 = 1
=> a2b2 + a2c2 + b2c2 = 1 ( * )
Ta có: a2 + b2 + c2 = 2
=> ( a2 + b2 + c2 )2 = 22
=> a4 + b4 + c4 + 2a2b2 + 2a2c2 + 2b2c2 = 4
=> a4 + b4 + c4 + 2( a2b2 + a2c2 + b2c2 ) = 4
Từ ( * ) => a4 + b4 + c4 + 2 x 1 = 4
=> a4 + b4 + c4 = 4 - 2 = 2
~~~~
Phần còn lại tương tự, cậu tự làm nhóe :3 Chúc cậu học tốt ~~

\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\Leftrightarrow\frac{ab+bc+ca}{abc}=0\Rightarrow ab+bc+ca=0\\ \)
\(\Rightarrow bc=-ab-ac,ca=-ab-bc,ab=-bc-ca\)
\(\Rightarrow\frac{a^2+bc}{a^2+2bc}=\frac{a^2+bc}{a^2+bc+bc}=\frac{a^2+bc}{a^2+bc-ca-ab}=\frac{a^2+bc}{\left(a-b\right).\left(a-c\right)}\)
Làm tương tự. có: \(\frac{b^2+ca}{b^2+2ca}=\frac{b^2+ca}{b^2+ca-ab-bc}=\frac{b^2+ca}{\left(a-b\right).\left(c-b\right)}\)
\(\frac{c^2+ab}{c^2+2ab}=\frac{c^2+ab}{c^2+ab-ca-bc}=\frac{c^2+ab}{\left(b-c\right).\left(a-c\right)}\)
\(\Rightarrow A=\frac{a^2+bc}{\left(a-b\right).\left(a-c\right)}+\frac{b^2+ca}{\left(a-b\right).\left(c-b\right)}+\frac{c^2+ab}{\left(b-c\right).\left(a-c\right)}\)
\(=\frac{\left(a^2+bc\right).\left(b-c\right)}{\left(a-b\right).\left(b-c\right).\left(a-c\right)}-\frac{\left(b^2+ca\right).\left(a-c\right)}{\left(a-b\right).\left(b-c\right).\left(a-c\right)}+\frac{\left(c^2+ab\right).\left(a-b\right)}{\left(a-b\right).\left(b-c\right).\left(a-c\right)}\)
Sau đó bạn thực hiện tiếp nhé.
Bài 1: Cho \(a,b,c\ge0:a^2+b^2+c^2=3\). CMR: \(a^4b^4+b^4c^4+c^4a^4\le3\)
Bài 2: Cho \(a,b,c\ge0\). CMR: \(a^2+b^2+c^2+2abc+1\ge2\left(ab+bc+ca\right)\)
Bài 3: Cho \(a,b,c\ge0:a^2+b^2+c^2=a+b+c\). CMR: \(a^2b^2+b^2c^2+c^2a^2\le ab+bc+ca\)
Bài 4: Cho \(a,b,c\ge0\). CMR: \(4\left(a+b+c\right)^3\ge27\left(ab^2+bc^2+ca^2+abc\right)\)
Bài 5: Cho \(a,b,c\ge0:a+b+c=3\).CMR: \(\frac{1}{2bc^2+1}+\frac{1}{2ca^2+1}+\frac{1}{2ab^2+1}\ge1\)

\(a^2+b^2+c^2=\left(a+b+c\right)^2\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2ac+2bc=a^2+b^2+c^2\)
\(\Leftrightarrow2\left(ab+ac+bc\right)=0\)
\(\Leftrightarrow ab+ac+bc=0\)
\(\Leftrightarrow\hept{\begin{cases}ab=-ac-bc\\ac=-ab-bc\\bc=-ab-ac\end{cases}}\)
Ta có : \(a^2+2bc=a^2+bc+bc=a^2+bc-ab-ac=a\left(a-b\right)-c\left(a-b\right)=\left(a-b\right)\left(a-c\right)\)
CMTT ta có : \(\hept{\begin{cases}b^2+2ac=\left(b-a\right)\left(b-c\right)\\c^2+2ab=\left(c-a\right)\left(c-b\right)\end{cases}}\)
Thay vào A ta được :
\(A=\frac{1}{\left(a-b\right)\left(a-c\right)}+\frac{1}{\left(b-a\right)\left(b-c\right)}+\frac{1}{\left(c-a\right)\left(c-b\right)}\)
\(A=\frac{b-c}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}+\frac{-a+c}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}+\frac{a-b}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}\)
\(A=\frac{b-c-a+c+a-b}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}\)
\(A=\frac{0}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}\)
\(A=0\)