Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
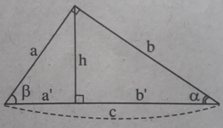
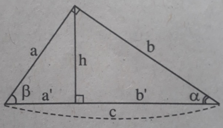
Với hai góc α và β mà α + β = 90 °
sin α = cos β ; cos α = sin β
tan α = cot β ; cot α = tan β

\(sin\alpha=cos\beta=\dfrac{AB}{BC}\)
\(tan\alpha=cot\beta=\dfrac{AB}{AC}\)
\(\alpha+\beta=90^o\)
\(\Rightarrow\beta=90^o-\alpha\)
Theo đề bài :
\(sin\alpha=cos\beta\)
\(\Rightarrow sin\alpha=cos\left(90^o-\alpha\right)\)
mà \(\alpha;90^o-\alpha\) là 2 góc phụ nhau
\(\Rightarrow cos\left(90^o-\alpha\right)=sin\alpha\left(dpcm\right)\)
Tương tự \(tan\alpha=cot\beta=cot\left(90^o-\alpha\right)\)

Lên cốc cốc tìm cốc cốc toán thay 2 vào mà tìm vậy cũng phải đăng


Với hai góc α và β mà α + β = 90o. Ta có:
sin α = cos α ; cos α = sin α
tan α = cot α ; cot α = tan α
Đáp án cần chọn là: B

\(\frac{1-tana}{1+tana}=\frac{1-\frac{sina}{cosa}}{1+\frac{sina}{cosa}}=\frac{\frac{1}{cosa}\left(cosa-sina\right)}{\frac{1}{cosa}\left(cosa+sina\right)}=\frac{cosa-sina}{cosa+sina}\)
Đáp án B
Với hai góc α và β mà α + β = 90 °
sin α = cos β ; cos α = sin β
tan α = cot β ; cot α = tan β