Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 5x = 8y = 20z => \(\dfrac{5x}{40}\)= \(\dfrac{8y}{40}\)=\(\dfrac{20z}{40}\)=> \(\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{z}{2}\)
áp dụng tính chất dãy tỉ số = nhau . Và x-y-z=3 .Ta có
\(\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{z}{2}\) =\(\dfrac{x-y-z}{8-5-2}\)=3
\(\dfrac{x}{8}\)=3 => x= 8.3
=> x = 24
\(\dfrac{y}{5}=3\)=> x = 5.3
=> x = 15
\(\dfrac{z}{2}\)=3 => x = 2.3
=> x =6
b ) (\(\dfrac{6}{11}\))x = (\(\dfrac{9}{2}\))y
---> x = (\(\dfrac{9}{2}\))(\(\dfrac{11}{6}\))y = (\(\dfrac{33}{4}\))y
(\(\dfrac{9}{2}\))y = (\(\dfrac{18}{5}\))z
---> z = (\(\dfrac{9}{2}\))(\(\dfrac{5}{18}\))y = (\(\dfrac{5}{4}\))y
---> - x + y + z = (\(\dfrac{-33}{4}\))y + y + (\(\dfrac{5}{4}\))y = - 120
---> - 6y = - 120 ---> y = 20 ---> x = 165 và z = 25.

Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{y+x+t}=\dfrac{y}{z+t+x}=\dfrac{y}{t+x+y}=\dfrac{t}{x+y+z}=\dfrac{x+y+z+t}{3\left(x+y+z+t\right)}=\dfrac{1}{3}\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+z=3t\\y+z+t=3x\\z+t+x=3y\\t+x+y=3z\end{matrix}\right.\)
\(\Rightarrow x=y=z=t\)
Thay vào P ta được :
\(P=1+1+1+1=4\)

Câu 2:
\(\dfrac{3^{3x}+3^{3x+2}}{3^3}=\dfrac{4^{2x+1}+4^{2x}}{2^3}\)
\(\Rightarrow\dfrac{3^{3x}\left(1+3^2\right)}{3^3}=\dfrac{4^{2x}\left(4^1+1\right)}{2^3}\)
\(\Rightarrow\dfrac{27^x.10}{27}=\dfrac{16^x.5}{8}\Rightarrow27^{x-1}.10=16^{x-1}.10\)
\(\Rightarrow27^{x-1}=16^{x-1}\)
Vì \(27\ne16\) và \(27;16\in N\)* nên
\(x-1=0\Leftrightarrow x=1\)
Vậy...................
Chúc bạn học tốt!!!
\(\left\{{}\begin{matrix}xy=-2\\yz=-3\\xz=6\end{matrix}\right.\) \(\Leftrightarrow xy.yz.xz=36\Leftrightarrow\left(xyz\right)^2=36\Leftrightarrow xyz=6\)
\(\Leftrightarrow\left\{{}\begin{matrix}z=-3\\x=-2\\x=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}z^2=9\\x^2=4\\x^2=1\end{matrix}\right.\)
\(\Leftrightarrow x^2+y^2+z^2=9+4+1=12\)

Trả lời :
Bn tham khảo đường link này nhé ^^
Câu hỏi của khongcanten - Toán lớp 7 - Học toán với OnlineMath
Chúc bn hc tốt <3
x O y z t
Ta có : \(\widehat{xOt}\)và \(\widehat{xOz}\)là 2 góc kề bù nên \(\widehat{xOt}+\widehat{xOz}=180^o\)( tc góc kề bù )
mà \(\widehat{xOt}=4\widehat{xOz}\)
Do đó \(4\widehat{xOt}+\widehat{xOz}=180^o\)hay \(5\widehat{xOz}=180^o\)
Vậy \(\widehat{xOz}=180^o:5=36^o\)
Suy ra \(\widehat{xOt}=4.36^o=144^o\)
Các cặp góc \(\widehat{yOz}\)và \(\widehat{xOt}\), \(\widehat{tOy}\)và \(\widehat{xOz}\)là các cặp góc đổi đỉnh do đó:
\(\widehat{yOz}=\widehat{xOt}=144^o\)
\(\widehat{tOy}=\widehat{xOz}=36^o\)
Chúc bạn học tốt !!!

\(\left\{{}\begin{matrix}x\left(x+y+z\right)=7\\y\left(x+y+z\right)=3\\z\left(x+y+z\right)=15\end{matrix}\right.\) (đoán là đề vậy thôi vì bạn viết thiếu)
\(\Rightarrow x\left(x+y+z\right)+y\left(x+y+z\right)+z\left(x+y+z\right)=7+3+15\)\(\Rightarrow\left(x+y+z\right)\left(x+y+z\right)=25\)
\(\Rightarrow\left(x+y+z\right)^2=25\)
\(\Rightarrow x+y+z=\pm5\)
....
\(\left\{{}\begin{matrix}xy=\dfrac{6}{7}\\yz=\dfrac{7}{12}\\xz=2\end{matrix}\right.\)
\(\Rightarrow xy.yz.xz=\dfrac{6}{7}.\dfrac{7}{12}.2\)
\(\Rightarrow xyz^2=1\)
\(\Rightarrow xyz=\pm1\)
...
tìm x,y,z
a,x(x+y+z)=7,y(x+y+z)=3,z(x+y+z)x(x+y+z)=7,y(x+y+z)=3,z(x+y+z)=6
b,xy=67,yz=712,xz=2

Ta có:\(\frac{x}{x+y+z}< \frac{x+t}{x+y+z+t};\frac{y}{x+y+t}< \frac{y+z}{x+y+z+t};\frac{z}{y+z+t}< \frac{z+x}{x+y+z+t};\frac{t}{x+z+t}< \frac{t+y}{x+y+z+t}\)
Khi đó:\(M< \frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}\)
\(=\frac{2\left(x+y+z+t\right)}{x+y+z+t}\)
\(=2\)
\(\Rightarrow M^{10}< 2^{10}=1024< 2020\)
Vậy ta có điều fải chứng minh :D

Với mọi x thuộc R Có (x^2-9)^2 \(\ge\) 0
[y-4] \(\ge\) 0
Suy ra (x^2-9)^2+[y-4] - 1 \(\ge\) -1
Xét A=-1 khi và chỉ khi (x^2-9)^2 và [y-4] đều bằng 0
Tự tính ra
Xin lỗi nhưng vì không biết nên mình phải dùng [ ] thay cho GTTĐ nhé
Xin lỗi nhiều tại mình o tìm được kí hiệu đó
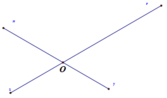
Ta có x O t ^ = 4 z O x ^ (gt) mà x O t ^ + x O z ^ = 180 ° suy ra x O z ^ = 36 ° , x O t ^ = 144 °