Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Khi có góc lệch cực tiểu đối với ánh sáng
vàng thì r1v = r2v = 0,5A = 0,5.500 = 250.
→ Góc tới sini1v = nvsinr1v
→ sini1v = 1,52sin250→ i1v = 400 .
+ Với ánh sáng đỏ, ta có sini1 = nsinr1
→ sin400 = 1,5sinr1 → r1 = 25,370.
A = r1 + r2 → r2 = 500 – 25,370 = 24,630.
+ Tại mặt bên thứ hai nsinr2 = sini2
→ 1,5.sin24,630 = sini2 → i2 = 38,690.
→ Góc lệch của tia đỏ ra khỏi lăng kính
D = i1 + i2 – A= 400 + 38,690 – 500 = 28,70.

Góc lệch ∆D giữa tia đỏ và tia tím :
∆D = (nt -nđ)A = (1,685 - 1,643).5° =.0,21° = 12,6'

Tia đỏ có tia ló đối xứng qua mặt phân giác --> Tia đỏ có góc lệch cực tiểu, khi đó, bạn vẽ hình ra sẽ tìm được góc tới i1
sin i1 / sin 300 = căn 2 --> i1 = 450.
Sau đó, áp dụng công thức thấu kính để tìm góc r2, bạn sẽ thấy xảy ra phản xạ toàn phần với một phần tia sáng --> Tia màu tím không ló ra được
--> Đáp án A sai.

Bạn hình dung lăng kính là một khối lăng trụ tam giác, nên góc chiết quang A nằm trên cạnh A. Còn khi nói AB là nói một mặt bên của lăng kính.
A M N i1 i2 r1 r2 60
+ Để có góc lệch cực tiểu thì góc tới i1 = góc ló i2, tam giác AMN đều
--> r1 = 300.
+ Tia màu đỏ
sini1 = n sin r1 --> i1 = 450
+ Tương tự, với tia màu tím: i1' = 600
Như vậy, góc quay: 60 - 45 = 150

a/ Chiết suất của lăng kính đối với tia tím và đỏ tính theo (1) là:
\(n_t=1,7311\text{≈}\sqrt{3};\)\(n_đ=1,4142\text{≈}\sqrt{2}\)
Khi góc lệch của tia tím là cực tiểu thì: \(\iota'_1=\iota_2\Rightarrow r_1=r_2=\frac{A}{2}\)
và \(D_{min}=2\iota_1-A\) hay \(\iota_1=\frac{D_{tmin}+A}{2}\)
áp dụng công thức : \(\sin\iota_1=n\sin r_1\) ta được \(\sin D_{tmin}+A_2=n_t\sin\frac{A}{2}\)
Đối với tia tím \(n_t=\sqrt{3}\) và biết \(A=60^0\), ta được:
\(\sin D_{tmin}+A_2=60^0\Rightarrow D_{tmin}=60^0\)
Góc tới của tia sáng trắng ở mặt AB phải bằng:\(i_t=60^0\)
b/ Tương tự như vậy, muốn cho góc lệch của tia đỏ là cực tiểu thì:
\(\sin\frac{D_{dmin}+A}{2}=n_d\sin\frac{A}{2}\Rightarrow D_{dmin}=30^0\)
và góc tới của tia sáng trắng trên mặt AB là: \(i_đ=45^0\)
Như vậy phải giảm góc tới trên mặt AB một góc là :\(i_t-t_đ=15^0\), tức là phải quay lăng kính quanh cạnh A một góc \(15^0\) ngược chiều kim đồng hồ.
c/Gọi \(r_{0đ}\)và \(r_{0t}\) là các góc giới hạn phản xạ toàn phần của tia đỏ và tia tím ta có:
\(\sin r_{0đ}=\frac{1}{n_d}=\frac{1}{\sqrt{2}}\Rightarrow r_{0đ}=45^0\)
\(\sin r_{0t}=\frac{1}{n_t}=\frac{1}{\sqrt{3}}\)=>r0t < r0đ .Do đó muốn cho không có tia sáng nào ló ra khỏi mặt AC của lăng kính thì phải có: r2 \(\ge\)r0đ \(\Rightarrow r_2\ge15^0\)
Hay \(\sin r_1\ge\sin\left(60^0-45^0\right)=0,2588\)
Biết \(\sin r_{1t}=\frac{\sin\iota}{n_t},\sin r_{1đ}=\frac{\sin\iota}{n_d}\); vì \(n_t\le n_đ\)nên suy ra \(r_{1t}\le\sin r_{1đ}\)(2)
Từ (1) và (2) ta thấy bất đẳng thức (1) được thõa mãn đối với mọi tia sáng, nghĩa là không có tia nào trong chùm sáng trắng ló ra khỏi mặt AC, nếu
\(\sin r_{1đ}\le0,2588\)hay \(\frac{\sin\iota}{n_đ}<0,2588\)
\(\Rightarrow\sin i\le0,2588.n_đ\)\(\Rightarrow\sin\le0,36\) .Suy ra góc tới:\(i\le21^06'\)

Chọn đáp án C.
δ = ( n t − n d ) A = ( 1 , 68 − 1 , 62 ) 6 0 = 0 , 36 0 ⇔ 0 , 006 ( r a d ) .
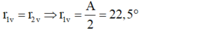
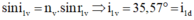
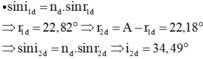
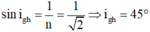
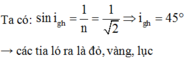
Chọn đáp án B