Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giả thiết => \(\frac{M\left(x-2\right)}{\left(x+1\right)\left(x-2\right)}+\frac{N\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}=\frac{32x-19}{\left(x+1\right)\left(x-2\right)}\)
=> M(x-2) + N(x+1) = 32x - 19
<=> M.x - 2.M + N.x + N = 32.x -19
=> (M+ N).x + (N - 2.M) = 32.x - 19
=> M+ N = 32 và -2M + N = -19
=> M = 17, N = 15
vậy M.N = 17. 15 =...

gọi độ dài cạnh hình vuông là a
=>a^2+a^2=(\(\sqrt{ }\)3)^2
=>2a^2=3
=>a^2=3/2
=>a=\(\sqrt{ }\)3/2

O B C D A DB=12cm AC=16cm
Gọi O là gđ 2 đường chéo AC và DB của hình thoi ABCD
Vì DB_|_AC=> OD_|_AC
=>OD là đường cao của tam giác ADC mà AD=DC (t/chất hình thoi)
=> OD là đường trung tuyến của tam giác ADC
=>OA=OC=AC=16/2= 8cm
=> OA=8cm
Vì: AC_|_DB=>OA_|_DB
=> OA là đường cao của tam giác ADB
Mà AD=AB ( theo t/chất hình thoi)
=>OA là đường trung tuyến của tam giác ADB
=>OD=OB=1/2DB=12/2=6cm
=>OD=6 cm
Áp dụng đl pitago vào tam giác vuông AOD có:
OA2+OD2=AD2
=>AD2=82+62
=> AD2=64+36
=> AD2=100
=> AD=5
Vậy độ dài cạnh hình thoi (AD)=5cm

Gọi độ dài cạnh của hv là a.
Theo đ/lí Pi-ta-go ta có:
a2 + a2 = \(\sqrt{3}^2\)=3
=> 2a2 = 3
=> a2 = 3/2 = 1,5
=> S hình vuông là 1,5.

A B C D
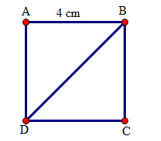
Gọi hình vuông ABCD có cạnh là 4 cm với đường chéo AD
có tam giác ACD vuông tại C
=> AC2+CD2=AD2 ( định lí Pitago)
42 .2=AD2
32=AD2
AD2=\(\sqrt{32}\)
Xét tam giác ABD vuông tại A, ta có:
BD2 = AB2 + AD2
BD2 = 42 + 42
BD2 = 16 + 16
BD2 = 32
BD = \(\sqrt{32}\)\(=4\sqrt{2}\left(cm\right)\)
Áp dụng định lý Py-ta-go ta tính được đường chéo của hình vuông:
Cạnh của hình vuông là:
\(\sqrt{\dfrac{\left(2a\right)^2}{2}}=\sqrt{\dfrac{4a^2}{2}}=\sqrt{2a^2}=\left|a\right|\sqrt{2}=a\sqrt{2}\)
Diện tích của hình vuông:
\(\left(a\sqrt{2}\right)^2=2a^2\)
Độ dài cạnh là:
\(\sqrt{\dfrac{\left(2a\right)^2}{2}}=a\sqrt{2}\)
Diện tích là;
\(\left(a\sqrt{2}\right)^2=2a^2\)