Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2) a) \(x^2-3=\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\)
b) \(x^2-6=\left(x-\sqrt{6}\right).\left(x+\sqrt{6}\right)\)
c) = \(x^2+2x.\sqrt{3}+\left(\sqrt{3}\right)^2=\left(x+\sqrt{3}\right)^2\)
d) = \(x^2-2x\sqrt{5}+\left(\sqrt{5}\right)^2=\left(x-\sqrt{5}\right)^2\)

\(a,5\sqrt{4a^6}-3a^3=5\left|2a^3\right|-3a^2=-10a^3-3a^3=-13a^3\)(vì a<0)
b)\(\sqrt{9a^4}+3a^2=\left|3a^2\right|+3a^2=3a^2+3a^2=6a^2\)
c)\(\frac{\sqrt{x^2-10x+25}}{x-5}=\frac{\left|x-5\right|}{x-5}\)
Với x-5>0 => x>5 => \(\frac{\sqrt{x^2-10x+25}}{x-5}=1\)
Với x-5<0=>x<5 =>\(\frac{\sqrt{x^2-10x+25}}{x-5}=-1\)

a, \(2\sqrt{a^2}-5a=2\left|a\right|-5a\)do a < 0
\(=-2a-5a=-7a\)
b, \(\sqrt{25a^2}+3a=\sqrt{\left(5a\right)^2}+3a=\left|5a\right|+3a\)do \(a\le0\)
TH1 : \(-5a+3a=-2a\)với \(a< 0\)
hoặc TH2 : \(5+3=8\)
c, \(\sqrt{9a^4}+3a^2=\sqrt{\left(3a^2\right)^2}+3a^2=\left|3a^2\right|+3a^2\)
\(=3a^2+3a^2=6a^2\)do \(3>0;a^2\ge0\forall a\Rightarrow3a^2\ge0\forall a\)
d, \(5\sqrt{4a^6}-3a^3=5\sqrt{\left(2a^3\right)^2}-3a^3\)
\(=5\left|2a^3\right|-3a^3=-10a^3-3a^3=-13a^3\)do \(a< 0\Rightarrow a^3< 0\)
a) \(2\sqrt{a^2}-5a\)=2\(|a|\)-5a = -2a-5a=-7a
b) \(\sqrt{25a^2}\) +3a = 5\(|a|\) + 3a=5a+3a=8a.
c) \(\sqrt{9a^4}\) + 3\(a^2\)=6\(a^2\)
d) \(5\sqrt{4a^6}\) - 3\(a^3\)=-13\(a^3\)
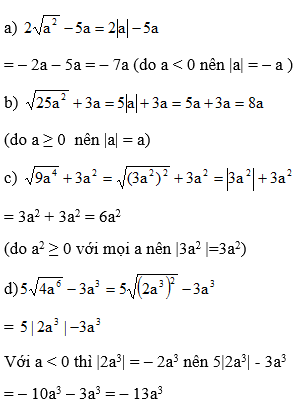
a) \(=5\left|a\right|+3a=5a+3a=8a\)
b) \(=3\left|a^2\right|+3a^2=3a^2+3a^2=6a^2\)
c) \(=5.2\left|a^3\right|-3a^3=-10a^3-3a^3=-13a^3\)
làm chi tiết cho em câu b đi ạ