Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(2ax-bx+3cx-2a+b-3c\\ =x\left(2a-b+3c\right)-\left(2a-b+3c\right)\\ =\left(x-1\right)\left(2a-b+3c\right)\)
\(ax-bx-2cx-2a+2b+4c\\ =x\left(a-b-2c\right)-2\left(a-b-2c\right)\\ =\left(x-2\right)\left(a-b-2c\right)\)
\(3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\)
\(ax^2-bx^2-2ax+2bx-3a+3b\\ =x^2\left(a-b\right)-2x\left(a-b\right)-3\left(a+b\right)\\ =\left(x^2-2x-3\right)\left(a+b\right)\\ =\left(x+1\right)\left(x-3\right)\left(a+b\right)\)

\(1,2x^2-6xy+5x-15y\)
\(=2x\left(x-3y\right)+5\left(x-3y\right)\)
\(=\left(x-3y\right)\left(2x+5\right)\)
\(2,ax^{2\:}-3axy+bx-3by\)
\(=ax\left(x-3y\right)+b\left(x-3y\right)\)
\(=\left(x-3y\right)\left(ax+b\right)\)
\(3,5ax^2-3axy+3ay^2-3axy\) ( Đề sai )
Sửa : \(3ax^2-3axy+3ay^2-3axy\)
\(=3ax\left(x-y\right)+3ay\left(y-x\right)\)
\(=3ax\left(x-y\right)-3ay\left(x-y\right)\)
\(=3a\left(x-y\right)^2\)
\(4,4acx+4bcx+4ax+4bx\)
\(=4cx\left(a+b\right)+4x\left(a+b\right)\)
\(=4x\left(a+b\right)\left(c+1\right)\)
\(6,ax^{2\:}y-bx^2y-ax+bx+2a-2b\)
\(=x^2y\left(a-b\right)-x\left(a-b\right)+2\left(a-b\right)\)
\(=\left(a-b\right)\left(x^2y-x+2\right)\)
\(7,ax^{2\:}-bx^2-2ax+2bx-3a+3b\)
\(=x^2\left(a-b\right)-2x\left(a-b\right)-3\left(a-b\right)\)
\(=\left(a-b\right)\left(x^2-2x-3\right)\)
\(8,ax^{2\:}-5x^2-ax+5x+a-5\)
\(=x^2\left(a-5\right)-x\left(a-5\right)+\left(a-5\right)\)
\(=\left(a-5\right)\left(x^2-x+1\right)\)
\(9,ax+bx+cx-2a-2b+2c\) Đề sai
Sửa :\(ax+bx+cx-2a-2b-2c\)
\(=x\left(a+b+c\right)-2\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(x-2\right)\)
\(10,2ax-bx+3cx-2a+b-3c\)
\(=\left(2ax-2a\right)-\left(bx-b\right)+\left(3cx-3c\right)\)
\(=2a\left(x-1\right)-b\left(x-1\right)+3c\left(x-1\right)\)
\(=\left(x-1\right)\left(2a-b+3c\right)\)
Mấy câu đề sai mk sửa chỗ nào ko đúng thì nói mk nha !

Lời giải:
31.
\(2a^2x-5by-6a^2y+2bx=(2a^2x+2bx)-(5by+5a^2y)\)
\(=2x(a^2+b)-5y(b+a^2)=(a^2+b)(2x-5y)\)
34.
\(4acx+4bcx+4ax+4bx=4x(ac+bc+a+b)\)
\(=4x[(ac+bc)+(a+b)]=4x[c(a+b)+(a+b)]=4x(c+1)(a+b)\)
37. Sửa đề:
\(2ax^2-bx^2-2ax+bx+4a-2b\)
\(=(2ax^2-bx^2)-(2ax-bx)+(4a-2b)\)
\(=x^2(2a-b)-x(2a-b)+2(2a-b)=(2a-b)(x^2-x+2)\)
Câu 31:
\(2a^2x-5by-5a^2y+2bx\)
\(=2x\left(a^2+b\right)-5y\left(a^2+b\right)\)
\(=\left(a^2+b\right)\left(2x-5y\right)\)
Câu 34:
\(4acx+4bcx+4ax+4bx\)
\(=4cx\left(a+b\right)+4x\left(a+b\right)\)
\(=\left(a+b\right)\left(4cx+4x\right)\)
\(=4x\left(a+b\right)\left(c+1\right)\)
Câu 37:
\(2ax^2-bx^2-2ax+bx+4a-2b\)
\(=x^2\left(2a-b\right)-x\left(2a-b\right)+2\left(2x-b\right)\)
\(=\left(2a-b\right)\left(x^2-x+2\right)\)
\(=\left(2a-b\right)\left(x^2-x+2\right)\)

d) \(ax^2-5x^2-ax+5x+a-5=\left(ax^2-ax+a\right)+\left(-5x^2+5x-5\right)\)
\(=a\left(x^2-x+1\right)-5\left(x^2-x+1\right)=\left(a-5\right)\left(x^2-x+1\right)\)
e) \(ax-bx-2cx-2a+2b+4c=x\left(a-b-2c\right)-2\left(a-b-2c\right)\)
\(=\left(x-2\right)\left(a-b-2c\right)\)

\(a,ax+by+ay+bx=\left(ax+ay\right)+\left(by+bx\right)=a\left(x+y\right)+b\left(x+y\right)=\left(a+b\right)\left(x+y\right)\)
\(b,x^2y+xy+x+1=xy\left(x+1\right)+\left(x+1\right)=\left(xy+1\right)\left(x+1\right)\)
\(c,x^2-ax-bx+ab=x\left(x-a\right)-b\left(x-a\right)=\left(x-b\right)\left(x-2\right)\)
\(d,x^2y+xy^2-x-y=xy\left(x+y\right)-\left(x+y\right)=\left(xy-1\right)\left(x+y\right)\)
\(e,a\left(x^2+y\right)-b\left(x^2+y\right)=\left(a-b\right)\left(x^2+y\right)\)
\(f,x\left(a-2\right)-a\left(a-2\right)=\left(x-a\right)\left(a-2\right)\)

Bài 2: Phân tích các đa thức sau thành nhân tử ( phương pháp nhóm hạng tử ) .
a) ax2 - 5x2 - ax + 5x + a - 5;
= ( ax2 - 5x2) - (ax - 5x) + (a - 5)
= x2(a - 5) - x(a - 5) + (a - 5)
= (a - 5) (x2 - x + 1)
b) ax - bx + cx - 3a + 3b - 3c
= ( ax - bx + cx) - (3a - 3b + 3c)
= x(a - b + c) - 3(a - b + c)
= (a - b + c)(x - 3)

A = xy + y - 2x - 2
= y( x + 1 ) - 2( x + 1 )
= ( x + 1 )( y - 2 )
B = x2 - 3x + xy - 3y
= x( x - 3 ) + y( x - 3 )
= ( x - 3 )( x + y )
C = 3x2 - 3xy - 5x + 5y
= 3x( x - y ) - 5( x - y )
= ( x - y )( 3x - 5 )
D = xy + 1 + x + y
= y( x + 1 ) + ( x + 1 )
= ( x + 1 )( y + 1 )
E = ax - bx + ab - x2
= ( ax - x2 ) + ( ab - bx )
= x( a - x ) + b( a - x )
= ( a - x )( x + b )
F = x2 + ab + ax + bx
= ( ax + x2 ) + ( ab + bx )
= x( a + x ) + b( a + x )
= ( a + x )( x + b )
G = a3 - a2x - ay + xy
= a2( a - x ) - y( a - x )
= ( a - x )( a2 - y )
Bonus : = ( a - x )[ a2 - ( √y )2 ]
= ( a - x )( a - √y )( a + √y )
H = 2xy + 3z + 6y + xz
= ( 6y + 2xy ) + ( 3z + xz )
= 2y( 3 + x ) + z( 3 + x )
= ( 3 + x )( 2y + z )
A = xy + y - 2x - 2 = y(x + 1) - 2(x + 1) = (y - 2)(x + !1
B = x2 - 3x + xy - 3y = x(x - 3) + y(x - 3) = (x + y)(x - 3)
C = 3x2 - 3xy - 5x + 5y = 3x(x - y) - 5(x - y) = (3x - 5)(x - y)
D = xy + 1 + x + y = xy + x + y + 1 = x(y + 1) + (y + 1) = (x + 1)(y + 1)
E = ax - bx + ab - x2 = ax - x2 + ab - bx = a(a - x) - b(a - x) = (a - b)(a - x)
F = x2 + ab + ax + bx = ab + ax + bx + x2 = a(b + x) + x(b + x) = (a + x)(b + x)
G = a3 - a2x - ay + xy = a2(a - x) - y(a - x) = (a2 - y)(a - x)
H = 2xy + 3z + 6y + xz = 2xy + 6y + 3z + xz = 2y(x + 3) + z(x + 3) = (2y + z)(x + 3)
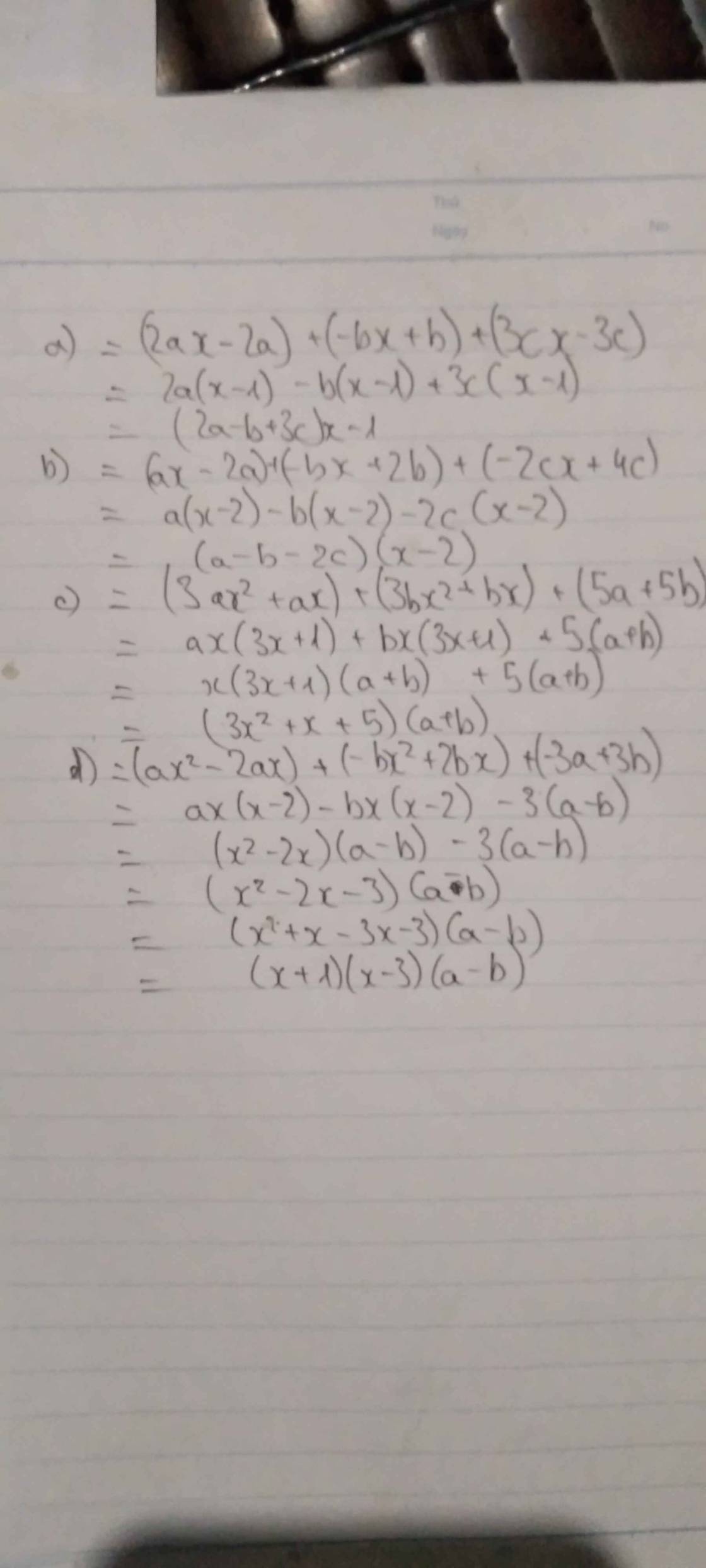
A = 4acx + 4bcx + 4ax + 4bx ( đã sửa '-' )
= 4x( ac + bc + a + b )
= 4x[ c( a + b ) + ( a + b ) ]
= 4x( a + b )( c + 1 )
B = ax - bx + cx - 3a + 3b - 3c
= x( a - b + c ) - 3( a - b + c )
= ( a - b + c )( x - 3 )
C = 2ax - bx + 3cx - 2a + b - 3c
= x( 2a - b + 3c ) - ( 2a - b + 3c )
= ( 2a - b + 3c )( x - 1 )
D = ax - bx - 2cx - 2a + 2b + 4c
= x( a - b - 2c ) - 2( a - b - 2c )
= ( a - b - 2c )( x - 2 )
E = 3ax2 + 3bx2 + ax + bx + 5a + 5b
= 3x2( a + b ) + x( a + b ) + 5( a + b )
= ( a + b )( 3x2 + x + 5 )
F = ax2 - bx2 - 2ax + 2bx - 3a + 3b
= x2( a - b ) - 2x( a - b ) - 3( a - b )
= ( a - b )( x2 - 2x - 3 )
= ( a - b )( x2 + x - 3x - 3 )
= ( a - b )[ x( x + 1 ) - 3( x + 1 ) ]
= ( a - b )( x + 1 )( x - 3 )