Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A: “Học sinh thích môn Bóng đá”
B: “Học sinh thích môn Bóng bàn”
Do đó ta có \(P\left( A \right) = \frac{{19}}{{30}},P\left( B \right) = \frac{{17}}{{30}},P\left( {AB} \right) = \frac{{15}}{{30}}\)
Theo công thức cộng xác suất
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{19}}{{30}} + \frac{{17}}{{30}} - \frac{{15}}{{30}} = \frac{{21}}{{30}} = \frac{7}{{10}}\)
Vậy xác suất để chọn được học sinh thích ít nhất một trong hai môn Bóng đá hoặc Bóng bàn là \(\frac{7}{{10}}\)

Kí hiệu A và B lần lượt là tập các học sinh đăng kí môn bóng đá và cầu lông.
Ta có A ∪ B = 40. Theo quy tắc cộng mở rộng ta có:
n (A ∩ B) = n(A) + n(B) − n(A ∪ B) = 30 + 25 - 40 = 15
Vậy có 15 em đăng kí chơi hai môn thể thao.

a) A = {Dung, Long, Cường, Trang}
B = {Lan, Hương, Phúc, Cường, Trang}
C = {Dung, Long, Lan, Hương, Phúc, Cường, Trang}
b) A ∪ B = {Dung, Long, Cường, Trang, Lan, Hương, Phúc}
a: A={Dung, Long, Cường, Trang}
B={Lan, Hương, Phúc, Cường, Trang}
C={Dung, Long, Lan, Hương, Phúc, Cường, Trang}
b: A hợp B={Dung,Long,Cường,Trang,Phúc,Hương,Lan}

Số học sinh thích cả bóng chuyền và bóng rổ là: 23 + 18 – 26 = 15 (học sinh)
Gọi A là biến cố “Học sinh thích bóng chuyền”; B là biến cố “Học sinh thích bóng rổ”; E là biến cố “Học sinh không thích cả bóng chuyền và bóng rổ”.
Khi đó \(\overline E \) là biến cố “Học sinh thích bóng chuyền hoặc bóng rổ”.
Ta có \(\overline E = A \cup B.\)
\(P\left( A \right) = \frac{{23}}{{40}},P\left( B \right) = \frac{{18}}{{40}} = \frac{9}{{20}},P\left( {AB} \right) = \frac{{15}}{{40}} = \frac{3}{8}\)
\(\begin{array}{l}P\left( {\overline E } \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{23}}{{40}} + \frac{9}{{20}} - \frac{3}{8} = \frac{{13}}{{20}}\\ \Rightarrow P\left( E \right) = 1 - P\left( {\overline E } \right) = 1 - \frac{{13}}{{20}} = \frac{7}{{20}}\end{array}\)
Vậy xác suất để chọn được học sinh không thích cả bóng chuyền và bóng rổ là \(\frac{7}{{20}}\).
Đáp án B.

Số học sinh thích cả bóng chuyền và bóng rổ là: 23 + 18 – 26 = 15 (học sinh)
Số học sinh thích bóng chuyền và không thích bóng rổ là 23 – 15 = 8 (học sinh)
Vậy xác suất để chọn được học sinh thích bóng chuyền và không thích bóng rổ là \(\frac{8}{{40}} = \frac{1}{5}\)
Đáp án C

a) \(P\left( A \right)\) là tỉ lệ học sinh học khá môn Ngữ văn trong tổng số học sinh của trường X
\(P\left( B \right)\) là tỉ lệ học sinh học khá môn Toán trong tổng số học sinh của trường X
\(P\left( {AB} \right)\) là tỉ lệ học sinh học khá cả hai môn Ngữ văn và Toán trong tổng số học sinh của trường X
\(P\left( {A \cup B} \right)\) là tỉ lệ học sinh học khá ít nhất một trong hai môn Ngữ văn và Toán trong tổng số học sinh của trường X
b) Ta không áp dụng được công thức \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\) vì hai biến cố A và B không độc lập với nhau do học sinh học khá môn Ngữ Văn có thể cũng học khá môn Toán (7% học sinh học khá cả hai môn Ngữ văn và Toán)

\(P\cup Q\): Học sinh đó hoặc bị cận thị hoặc giỏi môn toán
PQ: Học sinh đó vừa bị cận thị vừa giỏi môn Toán
\(\overline{PQ}\): Học sinh đó vừa không bị cận thị vừa không giỏi môn Toán

Gọi B là tập hợp “học sinh thích học Lý”
Gọi C là tập hợp ” học sinh thích học ít nhất một môn “
Ta có n(C) = n( A ∪ B) = n(A) + n(B) – n(A ∩ B) = 30 + 25 – 10 = 45
Vậy xác suất để được học sinh này thích học ít nhất là một môn Toán hoặc Lý là: 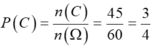
Chọn B.
Cặp biến cố E và F không xung khắc vì nếu học sinh được chọn thích môn Bóng đá thì cả E và F có thể xảy ra vì có 2 bạn thích cả hai môn Bóng đá và Cầu lông.
Vì có 2 bạn cùng thích bóng đá và cầu lông
nên hai biến cố E và F không xung khắc