Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

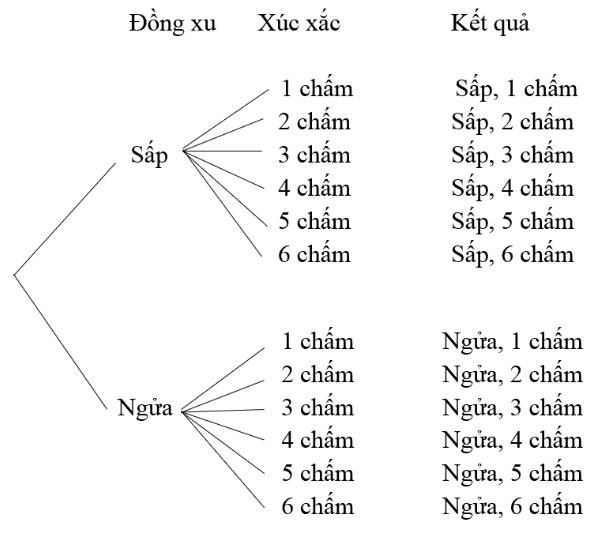
a) Kết quả của đồng xu và xúc xắc xảy ra đồng thời nên kết quả xảy ra gồm 2 kết quả liên tiếp nhau
Kết quả 1: Kết quả của đồng xu, có 2 kết quả: Sấp và ngửa
Kết quả 2: Kết quả của xúc xắc, có 6 kết quả: mỗi kết quả của mỗi mặt con xúc xắc
Áp dụng quy tắc nhân, ta có số kết quả có thẻ xuất hiện khi gieo đồng thời một đồng xu và một con xúc xắc là:
\(2.6 = 12\)
Vậy có 12 kết quả có thể xáy ra
b)

Để cam nhiều hơn thì sẽ có 3 th:
TH1: 2 cam, 1 mận, 1 xoài
=>Có \(C^2_8\cdot5\cdot4=560\)
TH2: 3 cam, 1 xoài
=>Có \(C^3_8\cdot4=224\left(cách\right)\)
TH3: 3 cam, 1 mận
=>Có \(C^3_8\cdot5=280\left(cách\right)\)
=>n(A)=280+224+560=1064
\(n\left(\Omega\right)=C^4_{17}=2380\)
=>P(A)=1064/2380=38/85

Chọn bất kì 6 quả cầu: \(C_{21}^6\) cách
Chọn 6 quả cầu sao cho ko có quả vàng nào (nghĩa là chọn 6 quả từ 13 quả xanh và đỏ): \(C_{13}^6\) cách
\(\Rightarrow\) Có \(C_{21}^6-C_{13}^6\) cách chọn 6 quả sao cho có ít nhất 1 quả vàng

Trong toán học, mỗi cách chọn 2 vận động viên từ 8 vận động viên để tạo thành một cặp đấu được gọi là một tổ hợp chập 2 của 8.

Giả sử chỉ có 1 quả cầu đỏ hoặc không có quả cầu đỏ nào
=>Có \(C^1_5\cdot C^5_{13}+C^0_5\cdot C^6_{13}=8152\left(cách\right)\)
Chọn 6 quả bất kì có \(C^6_{18}\left(cách\right)\)
=>Có \(18564-8152=10412\left(cách\right)\)

a) Chọn 3 cờ đỏ, trắng và xanh ta có 3 cách cắm để có 4 tín hiệu khác nhau là: ĐTX, ĐXT, TĐX, TXĐ
b) Việc cắm cờ để báo tín hiệu trên bao gồm 3 công đoạn
Công đoạn 1: Chọn cờ để cắm vào vị trí thứ nhất, có 5 cách chọn trong 5 màu khác nhau
Công đoạn 2: Chọn cờ để cắm vào vị trí thứ 2, có 4 cách chọn trong 4 màu còn lại
Công đoạn 3: Chọn cờ để cắm vào vị trí cuối cùng, có 3 cách chọn trong 3 màu còn lại
Áp dụng quy tắc nhân, ta có số cách cắm cờ để báo tín hiệu nhiều nhất là:
\(5.4.3 = 60\) (cách)


a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)
b) Thay \(t = 2\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.2 = 81\\y = 1 + 30.2 = 61\end{array} \right.\)
Vậy khi \(t = 2\) thì tọa độ của ô tô là \(\left( {81;61} \right)\)
Thay \(t = 4\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.4 = 161\\y = 1 + 30.4 = 121\end{array} \right.\)
Vậy khi \(t = 4\) thì tọa độ của ô tô là \(\left( {161;121} \right)\)




a) Việc chọn một quả dưa hấu hoặc một quả thanh long được thực hiện qua 2 phương án
Phương án 1: Chọn một quả dưa hấu, có 6 cách thực hiện
Phương án 2: Chọn một quả thanh long, có 15 cách thực hiện
Áp dụng quy tắc cộng, số cách chọn một quả dưa hấu hoặc một quả thanh long là
\(6 + 15 = 21\) (cách chọn)
b) Việc chọn một quả dưa hấu và một quả thanh long được thực hiện qua 2 công đoạn:
Công đoạn 1: Chọn một quả dưa hấu, có 6 cách thực hiện
Công đoạn 2: Chọn một quả thanh long, có 15 cách thực hiện
Áp dụng quy tắc nhân, số cách chọn một quả thanh long và một quả dưa hấu là
\(6.15 = 90\) (cách chọn)