Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là vị trí tàu thu tín hiệu. Gọi \({t_A},{t_B}\) lần lượt là thời gian tín hiệu truyền từ trạm phát A,B đến M. Theo đề bài, ta có \({t_A} - {t_B} = - 0,0005s\).
Suy ra \(MA - MB = v.{t_A} - v.{t_B} = 292000.\left( { - 0,0005} \right) = - 146km\).
Gọi (H) là hyperbol ở dạng chính tắc nhận A,B làm hai tiêu điểm và đi qua M. Khi đó ta có:
\(\left\{ \begin{array}{l}2a = \left| {MA - MB} \right| = 146\\2c = AB = 300\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\c = 150\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\{b^2} = {c^2} - {a^2} = 17171\end{array} \right.\)
Vậy phương trình chính tắc của (H) là: \(\frac{{{x^2}}}{{5329}} - \frac{{{y^2}}}{{17171}} = 1\).

Gọi M là vị trí phát ra âm thanh cầu cứu trong rừng.
Gọi \({t_1},{t_2}\)lần lượt là thời gian trạm A, B nhận được tín hiệu cầu cứu (đơn vị: giây)
\( \Rightarrow {t_A} = {t_B} - 6 \Leftrightarrow {t_B} - {t_A} = 6\)
Đổi \(v = 1{\rm{ }}236{\rm{ }}km/h{\rm{ }} = \frac{{\;1236}}{{3600}}km/s = \frac{{103}}{{300}}km/s.\;\)
Ta có: \(MA = {t_A}.v;MB = {t_B}.v\)
\( \Rightarrow MB - MA = ({t_B} - {t_A}).v = 6.\frac{{103}}{{300}} = 2,06(km)\)
Như vậy, tập hợp các điểm M là một hypepol nhận A, B làm hai tiêu điểm.
Ta có: \(AB = 16 = 2c \Rightarrow c = 8\); \(\left| {MA - MB} \right| = 2,06 = 2a \Rightarrow a = 1,03\)
\( \Rightarrow {b^2} = {c^2} - {a^2} = {8^2} - 1,{03^2} = 62,9391\)
Vậy phương trình chính tắc của hypebol đó là: (H) \(\frac{{{x^2}}}{{1,0609}} - \frac{{{y^2}}}{{62,9391}} = 1\)
Do MA < MB nên M thuộc của nhánh (H) gần A.
Vậy phạm vi tìm kiếm vị trí phát ra âm thanh đó là nhánh gần A của hypebol (H) có phương trình \(\frac{{{x^2}}}{{1,0609}} - \frac{{{y^2}}}{{62,9391}} = 1\).

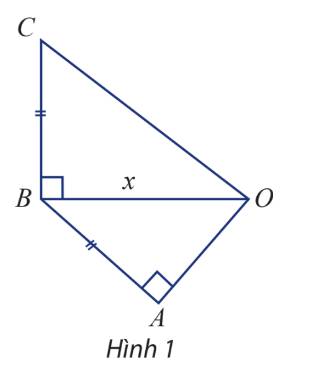
Gọi độ dài cạnh OB là x cm \(\left( {x > 0} \right)\)
Theo giả thiết ta có \(AB = BC = OB - 1 = x - 1\)
Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có:
\(OC = \sqrt {O{B^2} + B{C^2}} = \sqrt {{x^2} + {{\left( {x - 1} \right)}^2}} = \sqrt {2{x^2} - 2x + 1} \)
\(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{x^2} - {{\left( {x - 1} \right)}^2}} = \sqrt {2x - 1} \)
a) \(OC = 3OA \Rightarrow \sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = 9\left( {2x - 1} \right)\\ \Rightarrow 2{x^2} - 20x + 10 = 0\end{array}\)
\( \Rightarrow \)\(x = 5 - 2\sqrt 5 \) và \(x = 5 + 2\sqrt 5 \)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \) ta thấy cả hai đều thỏa mãn phương trình
Vậy khi \(OB = 5 - 2\sqrt 5 \) hoặc \(OB = 5 + 2\sqrt 5 \)thì \(OC = 3OA\)
b) \(OC = \frac{5}{4}OB \Rightarrow \sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = \frac{{25}}{{16}}{x^2}\\ \Rightarrow \frac{7}{{16}}{x^2} - 2x + 1 = 0\end{array}\)\(\)
\( \Rightarrow x = \frac{4}{7}\) hoặc \(x = 4\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(OB = \frac{4}{7}\) hoặc \(OB = 4\) (cm) thì \(OC = \frac{5}{4}OB\)

Gọi J là vị trí âm thanh phát đi. Ta có J cách đều O, A, B. Do đó J là giao của hài đường trun trực \({d_1},{d_2}\) tương ứng của OA, OB. Đường thẳng \({d_1}\) đi qua trung điểm M của OA và vuông góc với OA. Ta có \(M\left( {\frac{1}{2};0} \right)\) và \(\overrightarrow {{n_{{d_1}}}} = \overrightarrow {OA} = \left( {1;0} \right)\).
Phương trình đường thẳng \({d_1}\) là \(1\left( {x - \frac{1}{2}} \right) + 0\left( {y - 0} \right) = 0 \Leftrightarrow x = \frac{1}{2}\).
Tương tự, phương trình đường thẳng \({d_2}\) là \(x + 3y - 5 = 0\).
Tọa độ điểm J là nghiệm của hệ \(\left\{ \begin{array}{l}x = \frac{1}{2}\\x + 3y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = \frac{3}{2}\end{array} \right.\).
Vậy \(J\left( {\frac{1}{2};\frac{3}{2}} \right)\).

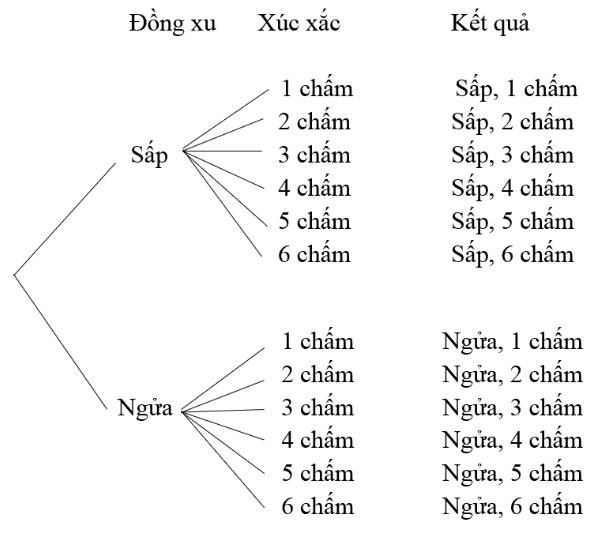
a) Kết quả của đồng xu và xúc xắc xảy ra đồng thời nên kết quả xảy ra gồm 2 kết quả liên tiếp nhau
Kết quả 1: Kết quả của đồng xu, có 2 kết quả: Sấp và ngửa
Kết quả 2: Kết quả của xúc xắc, có 6 kết quả: mỗi kết quả của mỗi mặt con xúc xắc
Áp dụng quy tắc nhân, ta có số kết quả có thẻ xuất hiện khi gieo đồng thời một đồng xu và một con xúc xắc là:
\(2.6 = 12\)
Vậy có 12 kết quả có thể xáy ra
b)

Số cách lấy ra là:
\(C^1_3\cdot C^3_9+C^2_3\cdot C^2_9+C^3_3\cdot C^1_9=369\left(cách\right)\)

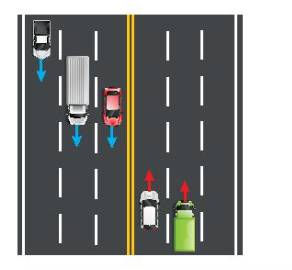
a) Các làn đường song song với nhau: Đúng.
b) Các xe chạy theo cùng một hướng: Sai.
Trong hình 4.5: Có 3 xe chạy theo hướng từ trên xuống dưới, 2 xe chạy thep hướng từ dưới lên trên
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau: Đúng.

a: Số cách chọn là \(C^6_{16}=8008\left(cách\right)\)
b: Số cách chọn là \(C^2_4\cdot C^4_{12}=2970\left(cách\right)\)
c: SỐ cách chọn là \(C^6_9+C^6_{12}+C^6_{11}=1470\left(cách\right)\)

a) Chọn 3 cờ đỏ, trắng và xanh ta có 3 cách cắm để có 4 tín hiệu khác nhau là: ĐTX, ĐXT, TĐX, TXĐ
b) Việc cắm cờ để báo tín hiệu trên bao gồm 3 công đoạn
Công đoạn 1: Chọn cờ để cắm vào vị trí thứ nhất, có 5 cách chọn trong 5 màu khác nhau
Công đoạn 2: Chọn cờ để cắm vào vị trí thứ 2, có 4 cách chọn trong 4 màu còn lại
Công đoạn 3: Chọn cờ để cắm vào vị trí cuối cùng, có 3 cách chọn trong 3 màu còn lại
Áp dụng quy tắc nhân, ta có số cách cắm cờ để báo tín hiệu nhiều nhất là:
\(5.4.3 = 60\) (cách)