Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{8}=\dfrac{b}{15}=\dfrac{c}{17}=\dfrac{a+b+c}{8+15+17}=\dfrac{120}{40}=3\)
Do đó: a=24; b=45; c=51
\(c^2=b^2+a^2\)
nên ΔABC vuông tại A

Với hình học bạn lưu ý chỉ nên đăng 1 bài 1 post. Đăng thế này khả năng bị bỏ qua bài rất cao, vì ai nhìn vào cũng thấy nản.

A B C M I N P
a) Ta có: \(BC=\sqrt{AB^2+AC^2}=10\)
\(\frac{PA}{PC}=\frac{BA}{BC}\Rightarrow\frac{PA}{CA}=\frac{BA}{BA+BC}\Rightarrow PA=\frac{BA.CA}{BA+BC}=\frac{6.8}{6+10}=3\)
\(BP=\sqrt{AB^2+AP^2}=3\sqrt{5}\)
\(\frac{BI}{PI}=\frac{AB}{AP}\Rightarrow\frac{BI}{BP}=\frac{AB}{AB+AP}\Rightarrow BI=\frac{AB.BP}{AB+AP}=\frac{6.3\sqrt{5}}{6+3}=2\sqrt{5}\)
Ta thấy: \(\frac{BI}{BM}=\frac{2\sqrt{5}}{5}=\frac{6}{3\sqrt{5}}=\frac{BA}{BP}\), suy ra \(\Delta BAP~\Delta BIM\)(c.g.c)
Vậy \(\widehat{BIM}=\widehat{BAP}=90^0.\)
b) Vẽ đường tròn tâm M đường kính BC, BI cắt lại (M) tại N.
Ta thấy \(\widehat{BIM}=\widehat{BNC}=90^0\), suy ra MI || CN, vì M là trung điểm BC nên I là trung điểm BN (1)
Dễ thấy \(\widehat{NIC}=\frac{1}{2}\widehat{ABC}+\frac{1}{2}\widehat{ACB}=\widehat{NCI}\), suy ra NI = NC (2)
Từ (1),(2) suy ra \(\tan\frac{\widehat{ABC}}{2}=\tan\widehat{NBC}=\frac{NC}{NB}=\frac{NI}{NB}=\frac{1}{2}\)
Suy ra \(\tan\widehat{ABC}=\frac{2\tan\frac{\widehat{ABC}}{2}}{1-\tan^2\frac{\widehat{ABC}}{2}}=\frac{4}{3}=\frac{AC}{AB}\)
\(\Rightarrow\frac{AC^2}{AB^2+AC^2}=\frac{16}{9+16}=\frac{16}{25}\Rightarrow\frac{AC}{BC}=\frac{4}{5}\)
Vậy \(AB:AC:BC=3:4:5\)
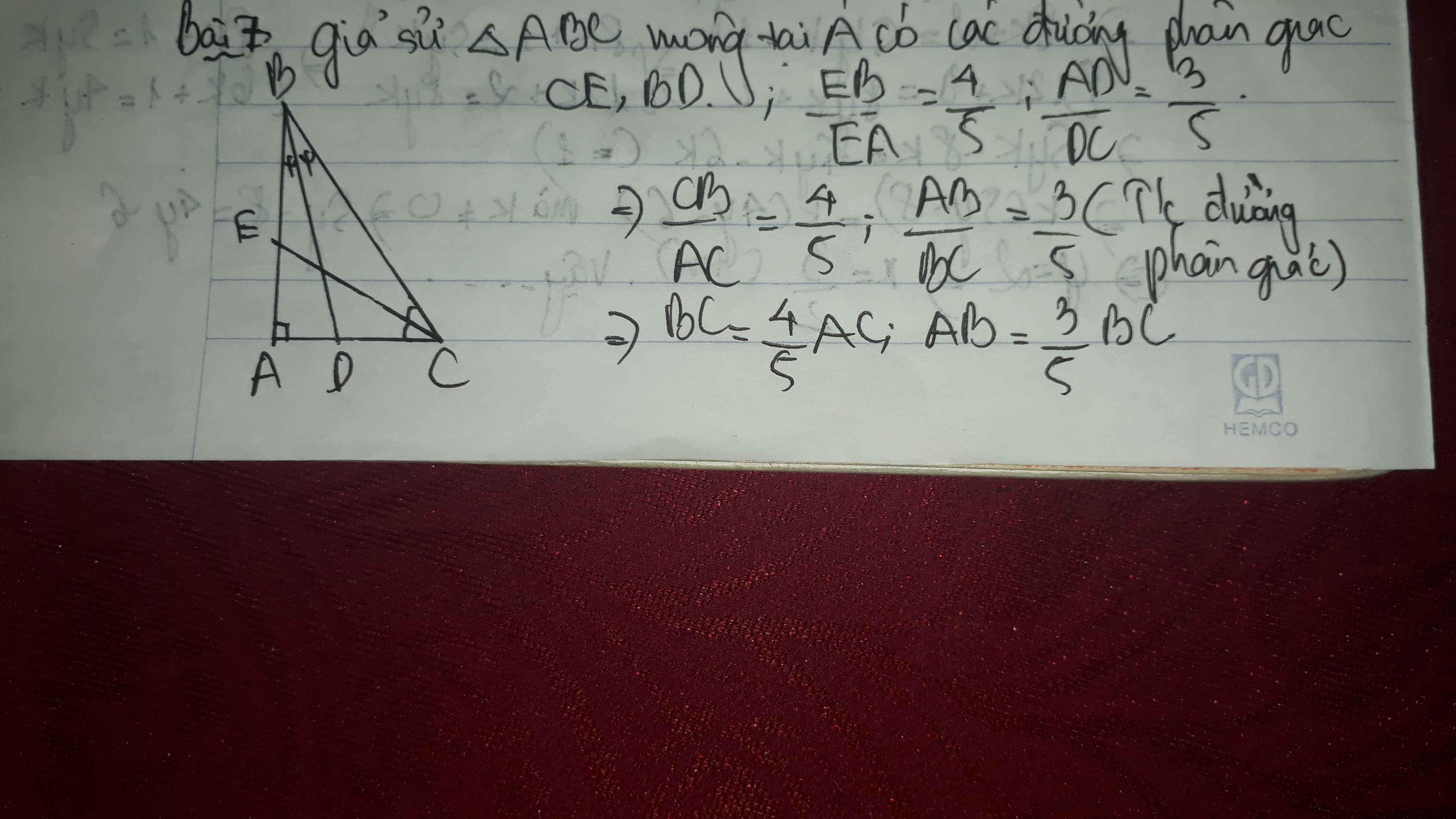
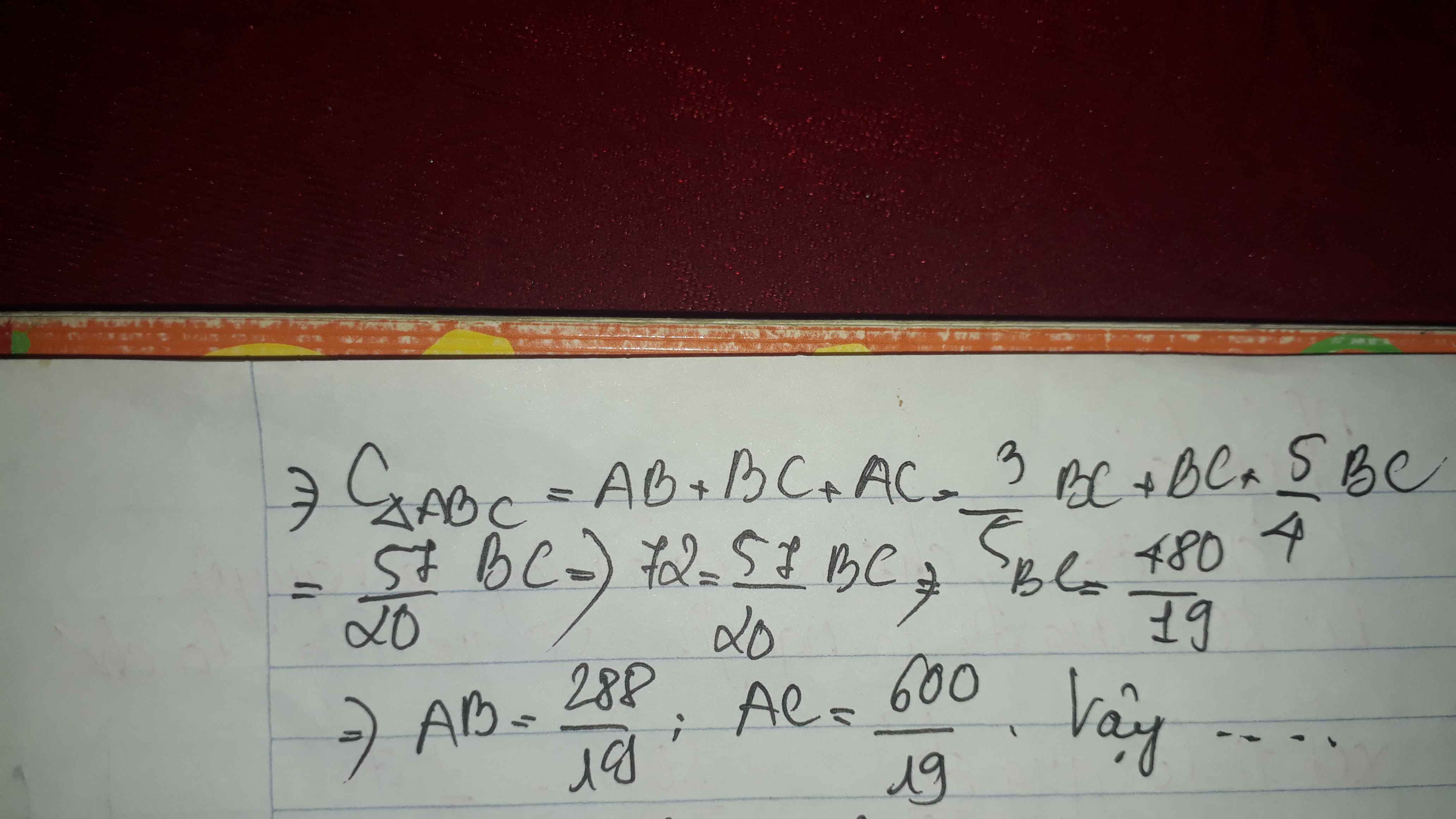

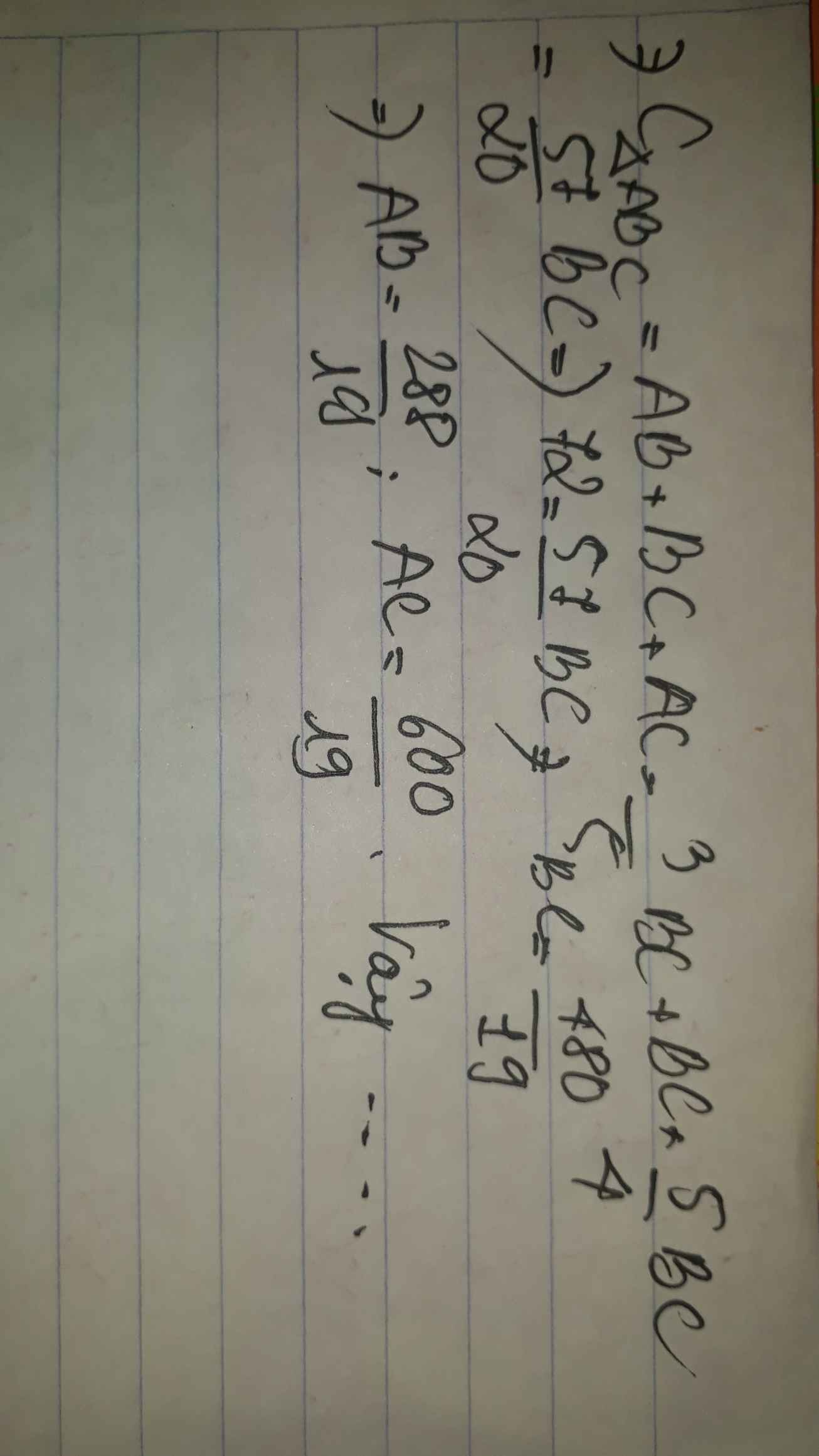
Ta có:
\(\hept{\begin{cases}a+b+c=49,49\\20a-21b=0\\29a-21c=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=14,14\\b=14,847\\c=20,503\end{cases}}\)
Giao điểm của ba đường phân giác chính là tâm của đường tròn nội tiếp.
Áp dụng công thức:
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=pr\left(p=\frac{a+b+c}{2}=\frac{49,49}{2}=24,745\right)\)
\(\Rightarrow r=\frac{\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}}{p}\)\(=\frac{\sqrt{24,745\left(24,745-14,14\right)\left(24,745-14,847\right)\left(24,745-20,503\right)}}{24,745}=4,242\)