Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi B(x; y) là vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.
Do tàu khởi hành từ A đi chuyển với vận tốc được biểu thị bởi vectơ \(\overrightarrow v = \left( {3;4} \right)\) nên cứ sau mỗi giờ, tàu đi chuyển được một quãng bằng \(\left| {\overrightarrow v } \right|\).
Vậy sau 1,5 giờ tàu di chuyển tới B, ta được: \(\overrightarrow {AB} = 1,5.\overrightarrow v \)
\(\begin{array}{l} \Leftrightarrow (x - 1;y - 2) = 1,5\;.\left( {3;4} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 4,5\\y - 2 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5,5\\y = 8\end{array} \right.\end{array}\)
Vậy sau 1,5 tàu ở vị trí (trên mặt phẳng tọa độ) là B(5,5; 8).

a)

b) Ta có: Tọa độ các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) lần lượt là: -5; 5
Ta có \(\overrightarrow {AB} = - \overrightarrow {CD} \)
Vậy hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ngược hướng

Tham khảo:

a) M thuộc cạnh BC nên vectơ \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \) ngược hướng với nhau.
Lại có: MB = 3 MC \( \Rightarrow \overrightarrow {MB} = - 3.\overrightarrow {MC} \)
b) Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \)
Mà \(BM = \dfrac{3}{4}BC\) nên \(\overrightarrow {BM} = \dfrac{3}{4}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {BC} \)
Lại có: \(\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \) (quy tắc hiệu)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)
Vậy \(\overrightarrow {AM} = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)

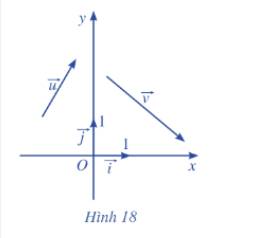
a) Do \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) nên \(\overrightarrow u = {x_1}\overrightarrow i + {y_1}\overrightarrow j .\), \(\overrightarrow v = {x_2}\overrightarrow i + {y_2}\overrightarrow j .\)
b) +) \(\overrightarrow u + \overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right) + \left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i + {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j + {y_2}\overrightarrow j } \right) = \left( {{x_1} + {x_2}} \right)\overrightarrow i + \left( {{y_1} + {y_2}} \right)\overrightarrow j \)
+) \(\overrightarrow u - \overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right) - \left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i - {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j - {y_2}\overrightarrow j } \right) = \left( {{x_1} - {x_2}} \right)\overrightarrow i + \left( {{y_1} - {y_2}} \right)\overrightarrow j \)
+) \(k\overrightarrow u = \left( {k{x_1}} \right)\overrightarrow i + \left( {k{y_1}} \right)\overrightarrow j \)
c) Tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)lần lượt là:
\(\left( {{x_1} + {x_2};{y_1} + {y_2}} \right),\left( {{x_1} - {x_2};{y_1} - {y_2}} \right),\left( {k{x_1},k{y_1}} \right)\)

a) Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \);
\(\overrightarrow b + \overrightarrow a = \overrightarrow {AE} + \overrightarrow {EC} = \overrightarrow {AC} \)
\( \Rightarrow \overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \)
b) Áp dụng quy tắc ba điểm ta có:
\(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)
\(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)

a) Sự khác biệt là:
- Đơn vị của 2 đại lượng: triệu đồng và km/h
- 20 triệu đồng là 1 đại lượng vô hướng còn cơn bão là đại lượng có hướng cụ thể là hướng từ đông sang bắc với vận tốc là 20 km/h
b) Các đại lượng cần biểu diễn vectơ là các đại lượng có hướng nên đó là: lực, độ dịch chuyển, vận tốc.
a) Sự khác biệt giữa hai đại lượng đã cho là:
- Bác Ba có số tiền là 20 triệu đồng, đại lượng này là một đại lượng vô hướng vì nó chỉ số tiền nên nó chỉ có độ lớn.
- Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc, đại lượng này là một đại lượng có hướng vì nó có đề cập đến độ lớn và hướng.
b) Trong các đại lượng đã cho, các đại lượng lực, độ dịch chuyển, vận tốc là các đại lượng có hướng, chúng bao gồm cả độ lớn và hướng nên các đại lượng đó cần được biểu diễn bởi vectơ.

a) Vật thể đi qua điểm \(A\left( {2;1} \right)\) và đi theo hướng vectơ \(\overrightarrow v \left( {3;4} \right)\).
b) Sau thời gian t thì vectơ vận tốc của vật thể là: \(t\overrightarrow v = \left( {3t;4t} \right)\).
Vậy tọa độ của vật thể sau thời gian t là: \(\overrightarrow {OA} + t\overrightarrow v = \left( {2 + 3t;1 + 4t} \right)\).

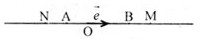
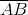 = 3;
= 3; 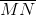 = -5. Từ đây ta có
= -5. Từ đây ta có 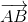 = 3
= 3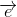 ,
, 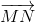 = -5
= -5
Ta thấy rô bốt đi từ A đến B, sau đó đi từ B đến C, vậy cả 2 lần di chuyển thì ta thấy điểm cuất phát là A và điểm kết thúc là C.
Suy ra vectơ biểu diễn sự dịch chuyển của rô bốt sau hai lần dịch chuyển là vectơ \(\overrightarrow {AC} \)