Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sự khác biệt là:
- Đơn vị đo: tấn và 500.
- Khối lượng hàng là đại lượng chỉ có độ lớn (500 tấn), còn độ dịch chuyển của tàu là đại lượng có cả độ lớn (500 km) và hướng (từ A đến B).

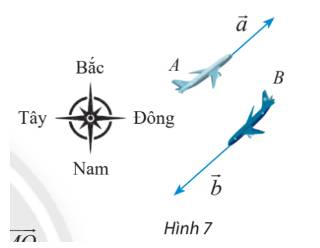
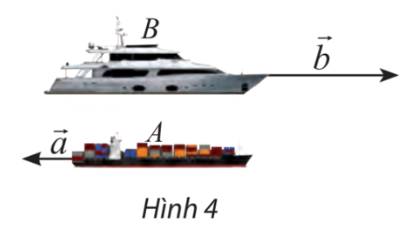
Vecto \(\overrightarrow a ,\;\overrightarrow b \) là vecto vận tốc của máy bay A và máy bay b.
Do đó \(\left| {\overrightarrow a } \right|,\;\left| {\overrightarrow b } \right|\) lần lượt là độ lớn của vecto vận tốc tương ứng.
Ta có: \(\left| {\overrightarrow a } \right| = 600,\;\left| {\overrightarrow b } \right| = 800\)
\( \Rightarrow \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{800}}{{600}} = \frac{4}{3}\)
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó \(\overrightarrow b = - \frac{4}{3}\overrightarrow a \)

Tham khảo:
Lấy các điểm: A, C sao cho:
Vectơ vận tốc dòng nước\(\overrightarrow {{v_n}} = \overrightarrow {OA} \)
Vectơ vận tốc chuyển động \(\overrightarrow {{v_{cano}}} = \overrightarrow {OC} \)
Ta có: \(\overrightarrow {{v_{cano}}} = \overrightarrow {{v_n}} + \overrightarrow v \), với \(\overrightarrow v \) là vectơ vận tốc riêng của cano.
Gọi B là điểm sao cho \(\overrightarrow v = \overrightarrow {OB} \) thì OACB là hình bình hành.

Vì tàu chuyển động theo hướng \(S{15^o}E\) nên vectơ \(\overrightarrow {OC} \) tạo với hướng Nam (tia OS) góc \({15^o}\) và tạo với hướng Đông (tia OE) góc \({90^o} - {15^o} = {75^o}\).
Mà nước trên sông chảy về hướng đông nên vectơ \(\overrightarrow {OA} \) cùng hướng với vectơ \(\overrightarrow {OE} \)
Do đó góc tạo bởi vectơ \(\overrightarrow {OC} \) và vectơ \(\overrightarrow {OA} \) là \({75^o}\)
Xét tam giác OAC ta có:
\(OA = \;|\overrightarrow {{v_n}} |\; = 3\); \(OC = \;|\overrightarrow {{v_{cano}}} |\; = 20\) và \(\widehat {AOC} = {75^o}\)
Áp dụng định lí cosin tại đỉnh O ta được:
\(\begin{array}{l}A{C^2} = O{A^2} + O{C^2} - 2.OA.OC.\cos \widehat {AOC}\\ \Leftrightarrow A{C^2} = {3^2} + {20^2} - 2.3.20.\cos {75^o} \approx 378\\ \Leftrightarrow OB = AC \approx 19,44\end{array}\)
Vậy vận tốc riêng của cano là 19,44 km/h

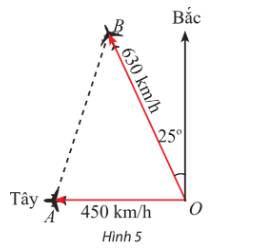
Ta có: \(\widehat {BOA} = {90^o} - {25^o} = {65^o}.\)
Sau 90 phút = 1,5 giờ:
Máy bay thứ nhất đi được quãng đường (OA) là: \(450.1,5 = 675\;(km)\)
Máy bay thứ hai đi được quãng đường (OB) là: \(630.1,5 = 945\;(km)\)
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos O\\ \Leftrightarrow A{B^2} = {675^2} + {945^2} - 2.675.945\cos {65^o}\\ \Rightarrow AB \approx 900\end{array}\)
Vậy sau 90 phút, hai máy bay cách nhau khoảng 900 km.

Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài \(\frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{50}}{{20}} = \frac{5}{2}\)
\( \Rightarrow \overrightarrow b = - \frac{5}{2}\overrightarrow a \)


a)
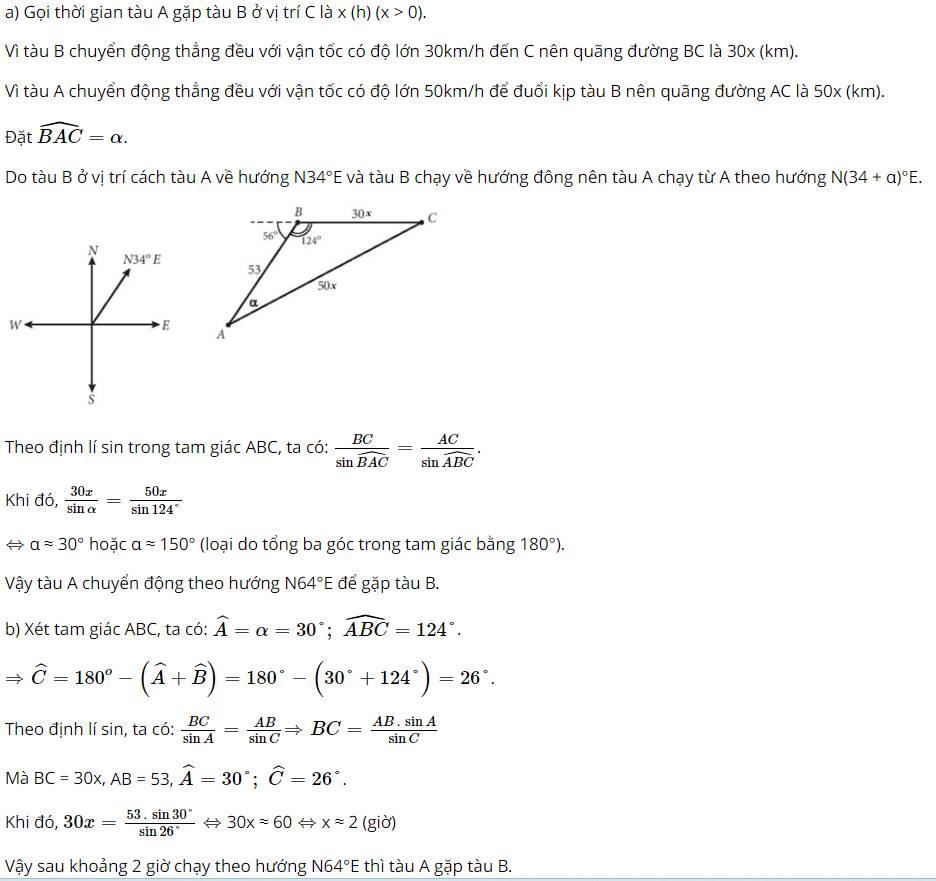
Gọi t (đơn vị: giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30km/h nên quãng đường BC = 30t
Tàu A đi với vận tốc có độ lớn 50km/h nên quãng đường AC = 50t
Theo định lí sin, ta có: \(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin B}}\)
Trong đó: \(\left\{ \begin{array}{l}a = BC = 30t\\b = AC = 50t\\\widehat B = {124^o}\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \frac{{30t}}{{\sin \alpha }} = \frac{{50t}}{{\sin {{124}^o}}}\\ \Leftrightarrow \sin \alpha = \frac{{30t.\sin {{124}^o}}}{{50t}} = \frac{{30.\sin {{124}^o}}}{{50}} \approx 0,4974\end{array}\)
\( \Leftrightarrow \alpha \approx {30^o}\) hoặc \(\alpha \approx {150^o}\)(loại)
Vậy tàu A chuyển động theo hướng tạo với vị trí ban đầu của tàu B góc \({30^o}\).
b) Xét tam giác ABC, ta có:
\(\begin{array}{l}\widehat B = {124^o};\widehat A = {30^o}\\ \Rightarrow \widehat C = {180^o} - \left( {\widehat B + \widehat A} \right) = {180^o} - \left( {{{124}^o} + {{30}^o}} \right) = {26^o}\end{array}\)
Theo định lí sin, ta có
\(\frac{a}{{\sin A}} = \frac{c}{{\sin C}} \Rightarrow a = \frac{{c.\sin A}}{{\sin C}}\)
Mà \(\left\{ \begin{array}{l}a = BC = 30t\\c = AB = 53\\\widehat A = {30^o};\widehat C = {26^o}\end{array} \right. \Rightarrow 30t = \frac{{53.\sin {{30}^o}}}{{\sin {{26}^o}}}\)
\(\begin{array}{l} \Leftrightarrow 30t \approx 60,45\\ \Leftrightarrow t \approx 2\;(h)\end{array}\)
Vậy sau khoảng 2 giờ thì tàu A đuổi kịp tàu B.

Ta thấy rô bốt đi từ A đến B, sau đó đi từ B đến C, vậy cả 2 lần di chuyển thì ta thấy điểm cuất phát là A và điểm kết thúc là C.
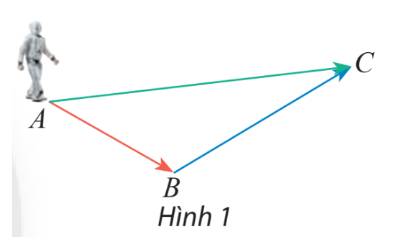
Suy ra vectơ biểu diễn sự dịch chuyển của rô bốt sau hai lần dịch chuyển là vectơ \(\overrightarrow {AC} \)

Gọi vectơ chỉ vận tốc của máy bay là vectơ \(\overrightarrow {AB} \) và vectơ chỉ vận tốc của gió là vectơ \(\overrightarrow {BC} \).
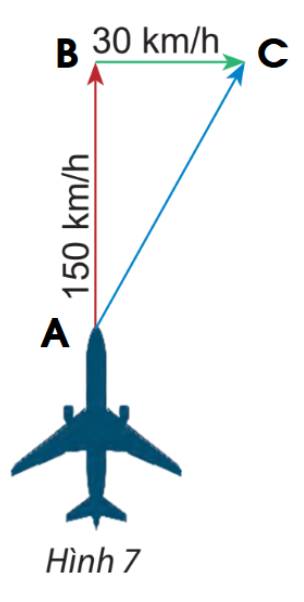
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Áp dụng định lý Pitago ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{150}^2} + {{30}^2}} = 30\sqrt {26} \)
Vậy độ dài vectơ tổng của hai vectơ nói trên là \(30\sqrt {26} \) km/h

a) Sự khác biệt là:
- Đơn vị của 2 đại lượng: triệu đồng và km/h
- 20 triệu đồng là 1 đại lượng vô hướng còn cơn bão là đại lượng có hướng cụ thể là hướng từ đông sang bắc với vận tốc là 20 km/h
b) Các đại lượng cần biểu diễn vectơ là các đại lượng có hướng nên đó là: lực, độ dịch chuyển, vận tốc.
a) Sự khác biệt giữa hai đại lượng đã cho là:
- Bác Ba có số tiền là 20 triệu đồng, đại lượng này là một đại lượng vô hướng vì nó chỉ số tiền nên nó chỉ có độ lớn.
- Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc, đại lượng này là một đại lượng có hướng vì nó có đề cập đến độ lớn và hướng.
b) Trong các đại lượng đã cho, các đại lượng lực, độ dịch chuyển, vận tốc là các đại lượng có hướng, chúng bao gồm cả độ lớn và hướng nên các đại lượng đó cần được biểu diễn bởi vectơ.