Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi x là thù lao người thợ chính nhận được trong 1 ngày (đồng)
y là thù lao người phụ chính nhận được trong 1 ngày (đồng)
ĐKXĐ:
0 < x,y < 11,7
Theo đề ta có:
- Một người thợ chính và một người thợ phụ đã nhận được một khoảng thù lao 11,7 triệu đồng sau khi hoàn thành xong công việc.Người thợ chính đã làm việc trong 15 ngày, còn người thợ phụ làm việc trong 14 ngày: 15x + 14y = 11,7 (1)
- Số tiền nhận được của thợ chính trong 4 ngày nhiều hơn số tiền nhận được của thợ phụ trong 3 ngày là 1,1 triệu đồng.
4x - 3y = 1,1 (2)
Từ (1) và (2) ta có hệ phương trình
\(\left\{{}\begin{matrix}15x+14y=11,7\\4x-3y=1,1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}20x+\frac{56}{3}y=\frac{78}{5}\\20x-15y=\frac{11}{2}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\frac{101}{3}y=\frac{101}{10}\\4x-3y=1,1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=0,3\\x=0,5\end{matrix}\right.\)
Vậy thợ chính nhận được 7,5 triệu đồng
thợ phụ nhận được 4,2 triệu đồng
Gọi thời gian người thứ nhất hoàn thành công việc khi làm một mình là x(giờ)(Điều kiện: x>24)
Thời gian người thứ hai hoàn thành công việc khi làm một mình là:
x-20(ngày)
Trong 1 ngày, người thứ nhất làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 ngày, người thứ hai làm được: \(\dfrac{1}{x-20}\)(công việc)
Trong 1 ngày, hai người làm được: \(\dfrac{1}{24}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{x-20}=\dfrac{1}{24}\)
\(\Leftrightarrow\dfrac{24\left(x-20\right)}{x\left(x-20\right)}+\dfrac{24x}{24x\left(x-20\right)}=\dfrac{x\left(x-20\right)}{24x\left(x-20\right)}\)
Suy ra: \(x^2-20x=24x-480+24x\)
\(\Leftrightarrow x^2-68x+480=0\)
\(\Delta=\left(-68\right)^2-4\cdot1\cdot480=2704\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{68-52}{2}=8\left(loại\right)\\x_2=\dfrac{68+52}{2}=\dfrac{120}{2}=60\left(nhận\right)\end{matrix}\right.\)
Vậy: Người thứ nhất cần 60 ngày để hoàn thành công việc khi làm một mình
Người thứ hai cần 40 ngày để hoàn thành công việc khi làm một mình
Gọi thời gian làm riêng của người 1 và người 2 lần lượt là a,b
Theo đề, ta có:
1/a+1/b=1/16 và 6/a+24/b=3/4
=>a=24 và b=48
Ket qua to1 lam duoc trong thang dau la420 sp
To2 lam duoc300sp
Gọi thời gian làm riêng của người 1 và người 2 lần lượtlà x,y
Theo đề, ta có: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{20}\\\dfrac{10}{x}+\dfrac{25}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=60\\y=30\end{matrix}\right.\)
Gọi số thợ cần thiết là x (người),x ∈ N* , thời gian cần thiết là y (ngày), y > 0.
Coi toàn bộ công việc như một đơn vị công việc, thì một người thợ trong 1 ngày làm được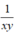 
( công việc).
Nếu giảm đi 3 người thì thời gian kéo dài 6 ngày. Như vậy, x – 3 người làm trong y + 6 ngày thì xong công việc. Do đó, ta có phương trình:
Nếu tăng thêm 2 người thì xong sớm 2 ngày. Như vậy, x + 2 người làm trong y – 2 ngày thì xong công việc. Do đó, ta có phương trình:
Từ (1) và (2) ta có hệ phương trình:
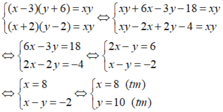
Vậy cần 8 người làm trong 10 ngày thì xong công việc.
Ta có sơ đồ :
Thợ cả |----------|----------|----------|----------|
Thợ phụ |----------|----------|----------|
Tổng số phần bằng nhau là :
5 + 3 = 8 ( phần )
Tiền lương của người thợ phụ là :
240 000 : 8 x 3 = 90 000 (đồng)
Tiền lương của người thợ cả là :
240 000 - 90 000 = 150 000 (đồng)
Đ/S : 90 000 đồng ; 150 000 đồng