Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với góc nhìn tạo với phương nằm ngang là 42 độ, ta có:
tan(42°) = h / 15
Để tìm giá trị của h, ta cần giải phương trình trên để tìm giá trị của h.
tan(42°) = h / 15
h = tan(42°) * 15
Sử dụng máy tính, ta tính được:
h ≈ 15.7m
Vậy, chiều cao của cây là khoảng 15.7m.

A B C E F
Gọi C là điểm đặt mắt người đó, BE là chiều cao của cây và CF là chiều cao người đó
Xét tứ giác AECF có:
\(\widehat{A}=\widehat{E}=\widehat{F}=90^0\)
=> AECF là hình chữ nhật
=> \(AE=CF=1,7m;AC=EF=30m\)
Áp dụng tslg trong tam giác ABC:
\(tanC=\dfrac{AB}{AC}\Rightarrow AB=30.tan35^0\approx21\left(m\right)\)
Chiều cao của cây: \(BE=AB+AE\approx21+1,7\approx23\left(m\right)\)
Lời giải:
Theo hình vẽ ta có:
$BC=DE=1,7$ (m)
$AB=BE.\tan \widehat{AEB}=30.\tan 35^0=21$ (m)
Chiều cao của cây là:
$AC=AB+BC=21+1,7=22,7$ (m)

Đáp án:
Giải thích các bước giải:
Giả sử AB là cây cần do, CD là cọc EF là khoảng cách từ mắt tới chân.
∆KDF ∽ ∆HBF
=> HBKD=HFKFHBKD=HFKF
=> HB = HF.KDKFHF.KDKF
mà HF = HK + KF =AC + CE = 15 + 0,8 = 15.8m
KD = CD – CK = CD – EF = 2 – 1,6 = 0,4 m
Do đó: HB = 7,9 m
Vậy chiều cao của cây là 7,9

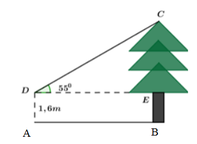
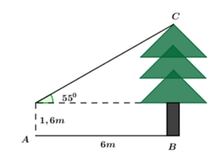
Đặt các điểm D, E như hình vẽ.
Xét CDE vuông tại E ta có:
![]()
Chiều cao của cây là BC = CE + BE = 8,57 + 1,6 = 10,17m
Đáp án cần chọn là: D

7: ΔABC vuông tại A có AB=12m; góc B=52 độ. Tính AC
AC=AB*tan52=12*tan52=15,36(m)