Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Quãng được vật đi được với vận tốc 3 \(km/h\)trong khoảng thời gian \(t\) (giờ) là:
\(s = v.t = 3.t\).
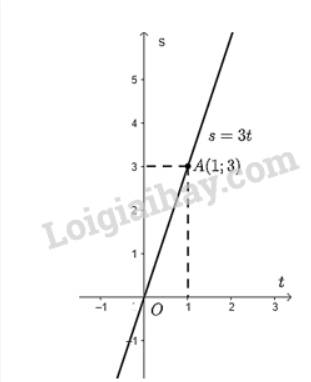
b) Vẽ đồ thị hàm số \(s = 3.t\)
Cho \(t = 1 \Rightarrow s = 3.1 = 3\)\( \Rightarrow \) đồ thị hàm số đi qua điểm \(M\left( {1;3} \right)\).
Đồ thị hàm số \(s = 3.t\) là đường thẳng đi qua hai điểm \(O\) và \(M\).

Cứ 1 giờ người đó lại đi được \(v\) km.
Cứ 2 giờ người đó lại đi được \(2v\)km.
Vậy sau \(t\left( h \right)\) người đó sẽ đi được quãng đường \(v.t\) km.
Vậy ta có công thức tính \(s\)theo \(t\) như sau: \(s = v.t\) trong đó \(v\) là vận tốc, \(t\) là thời gian và \(s\) là quãng đường đi được.

2) Gọi x = AB , C là điểm ô tô tăng tốc
=> thời gian dự định đi hết AB là \(\frac{x}{40}\)
Quãng đường ô tô đi với vận tốc 40km/h là AC \(=\frac{1}{2}-60\)
Thời gian đi là \(\left(\frac{x}{2}-60\right):40\)
Quãng đường ô tô đi với vận tốc 50km/h là CB =\(\frac{x}{2}+60\)
=> thời gian đi là \(\frac{\left(\frac{x}{2}+60\right)}{50}\)
Vì đến sớm hơn 1 giờ nên có pt : \(\frac{\left(\frac{x}{2}-60\right)}{40}+\frac{\left(\frac{x}{2}+60\right)}{50}=\frac{x}{40}-1\)
=> x = 2 × 40 + 50 − 60 + 60 = 280
=> x = 280

a) Hàm số biểu thị quãng đường S(t) (km) mà ô tô đi được trong thời gian t (h) là: S = 60t (km)
b) Quãng đường S(t) (km) mà ô tô đi được trong thời gian t = 2 (h) là: S = 60. 2= 120 (km)
quãng đường S(t) (km) mà ô tô đi được trong thời gian t = 3 (h) là: S = 60. 3 = 180 (km)

Ta có các biểu thức:
\(s=vt;v=\dfrac{s}{t};t=\dfrac{s}{v}\)
Tất cả đều là đơn thức không phải đa thức
`S = v.t; v = S/t; t = S/v`.
Không phải là đa thức.

| Vận tốc (km/h) | Quãng đường đi (km) | Thời gian đi (h) | |
| Xe máy | 35 | s | 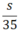 |
| Ô tô | 45 | 90 – s | 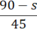 |
Ô tô xuất phát sau xe máy 2/5 giờ nên
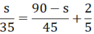

Vẽ đồ thị hàm số \(y = \dfrac{{ - 4}}{5}x\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(O\) và \(P\).
Từ điểm \(x = - 5\) trên \(Ox\)vẽ đường thẳng vuông góc với \(Ox\) cắt đồ thị hàm số tại điểm \(B\). Khi đó, điểm \(B\) là điểm trên đồ thị hàm số có hoành độ bằng -5.


Với \(v = 4 \Rightarrow s = 4t\). Khi đó \(s\) là hàm số bậc nhất theo biến \(t\).
Với \(t = 1 \Rightarrow s = 4.1 = 4 \Rightarrow \) đồ thị hàm số đi qua điểm \(A\left( {1;4} \right)\).
Đồ thị hàm số \(s = 4t\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(A\left( {1;4} \right)\).