Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số y tá của đoàn là x người và số bác sĩ là y người (x;y là các số nguyên dương)
Do số y tá nhiều hơn bác sĩ là 18 người nên: \(x-y=18\) (1)
Số y tá sau khi bớt 4 người: \(x-4\) người
Do khi đó số y tá bằng 3 lần số bác sĩ nên:
\(x-4=3y\Rightarrow x-3y=4\) (2)
Từ (1) và (2) ta có hệ:
\(\left\{{}\begin{matrix}x-y=18\\x-3y=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=25\\y=7\end{matrix}\right.\)

1) Gọi x, y lần lượt là số bác sĩ và y tá (x,y nguyên dương)
Theo đề bài ta có:
\(\hept{\begin{cases}x+y=45\\50x+35y=40\cdot45\end{cases}}\)
\(\hept{\begin{cases}x+y=45\\50x+35y=1800\end{cases}}\)
\(\hept{\begin{cases}x=30\\y=15\end{cases}}\)
\(\hept{\begin{cases}x=30\\y=15\end{cases}}\)
Vậy có 30 bác sĩ và 15 y tá.
2)
a. Ta có \(\widehat{AFH}=\widehat{AEH=90}độ\left(gt\right)\)
Nên \(\widehat{AFH}+\widehat{AEH=180}độ\)
Do đó tứ giác AEHF nội tiếp (tổng hai góc đối của 1 tứ giác bằng 180 độ)
Ta có \(\widehat{BFC}=\widehat{BEC}=90độ\left(gt\right)\)
Do đó tứ giác BCEF nội tiếp (2 đỉnh liên tiếp E, F cùng nhìn BC với 2 góc bằng nhau)

Gọi số bác sĩ là xx (người), số luật sư là yy (người). (x,y∈N∗;x;y<45)(x,y∈N∗;x;y<45)
Có 45 người gồm bác sĩ và luật sư nên ta có: x+y=45(1)x+y=45(1)
Tuổi trung bình của các bác sĩ là 35 nên ta có tổng số tuổi của các bác sĩ là 35x.35x.
Tuổi trung bình của các luật sư là 50 nên ta có tổng số tuổi của các luật sư là 50y.50y.
Mà tuổi trung bình của luật sư và bác sĩ là 40.40. Nên ta có phương trình
35x+50y45=40(2)35x+50y45=40(2)
Từ (1) và (2) ta có hệ phương trình:
{x+y=4535x+50y45=40⇔{x+y=4535x+50y=1800⇔{x=45−y35(45−y)+50y=1800⇔{x=45−y15y=225⇔{x=30y=15(tm)


Câu 1 :
Nửa chu vi miếng đất hình chữ nhật là: 100:2=50(m)
Gọi chiều dài miếng đất là: x(m)
chiều rộng miếng đất là: y(m)
(y<x<50)
Miếng đất hình chữ nhật có nửa chu vi là 50m .
=> Phương trình: x+y=50 (1)
5 lần chiều rộng hơn 2 lần chiều dài 40m.
\(\Rightarrow\) Phương trình : \(-2x+5y=40\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\hept{\begin{cases}x+y=50\\-2x+5y=40\end{cases}}\)
\(\hept{\begin{cases}y=50-x\\-2x+5\left(50-x\right)=40\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=50-x\\-2x+250-5x=40\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=50-x\\-2x-5x=40-250\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=50-x\\-7x=-210\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=50-30\\x=30\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=20\left(nhận\right)\\x=30\left(nhận\right)\end{cases}}\)
Vậy miếng đất hình chữ nhật có chiều dài là 30m và chiều rộng 20m
Câu 2 :
a) Gọi số người lớn trong gia đình bác Tú là: x(người)
Số trẻ em trong gia đình bác Tú là: y(người)
\(\left(y< x< 12\right)\left(x,y\inℕ^∗\right)\)
Gia đình bác Tú có 12 người.
=> Phương trình: x+y=12x (1)
Năm nay, gia đình bác dự định đi du lịch trong hè với tổng số tiền là 30 triệu đồng. Trong đó, mỗi người lớn chi phí cho chuyến đi hết 3 triệu, mỗi trẻ em chi phí hết 1,5 triệu.
=> Phương trình \(3x+1,5y=30\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\hept{\begin{cases}x+y=12\\3x+1,5y=30\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=8\left(nhận\right)\\y=4\left(nhận\right)\end{cases}}\)
Vậy gia đình bác Tú có 88 người lớn và 44 trẻ em.
b) Gọi số tiền mà mỗi người lớn phải trả trong chuyến du lịch đó hết x(triệu)
số tiền mà mỗi trẻ em phải trả trong chuyến du lịch đó hết y(triệu)
(y<x<43,6)
Năm ngoái, gia đình bác cũng với số người đó nhưng tiêu tốn chi phí cho cả chuyến du lịch của gia đình hết 43,6 triệu.
\(\Rightarrow\)Phương trình : \(x+y=43,6\left(1\right)\)
Mỗi người lớn chi phí nhiều hơn một trẻ em là 1,7 triệu.
\(\Rightarrow\) Phương trình : \(x-y=1,7\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\hept{\begin{cases}x+y=43,6\\x-y=1,7\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=22,65\left(nhận\right)\\y=20,95\left(nhận\right)\end{cases}}\)
Vậy trong chuyến du lịch đó chi phí cho mỗi người lớn là 22,65 triệu, trẻ em là 20,95 triệu.
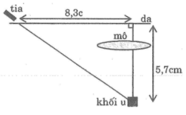
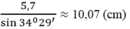
gọi số y tá là a,số bác sĩ là b(a,b thuộc N)
theo bài ra ta có: a-b=12 và b=(2/3)a
a-b=12 suy ra a=12+b
ta có: b=(2/3)a
=(2/3)(12+b)
=(2/3)x12+(2/3)xb=8+(2/3)b
b-(2/3)b=8 suy ra (1/3)b=8
vậy b=8/(1/3)=24
a=24+12=36
vậy có 24 bác sĩ và 36 y tá
Số bác sĩ là:
12 : (3 - 2) x 2 = 24(người)
Số y tá là:
24 : 2 x 3 = 36(người)
Đáp số: Bác sĩ: 24 người
Y tá :36 người