Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mặt phẳng khung dây hợp với đường cảm ứng từ một góc 300 => α= 600
\(\left|\phi\right|=\left|NBScos\alpha\right|=\left|1.5.10^{-2}.12.10^{-4}.cos60^0\right|=3.10^{-5}\)Wb

Vì tia sáng tới có đường kéo dài qua O nên tia tới SI vuông góc mặt phẳng trụ ⇒ góc i = 0 ⇒ tia sáng sẽ truyền thẳng vào khối trong suốt tới O.
Tại O: tia sáng SO tạo với pháp tuyến ON của mặt phân cách phẳng một góc tới i.
Ta có: i = 90o - α
Mặt khác, góc giới hạn khi ánh sáng truyền từ khối bán trụ ra không khí được tính bởi công thức:
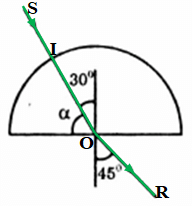
a) α = 60o
→ i = 90o – α = 30o → i < igh
Áp dụng định luật khúc xạ:
→ r = 45o. Vậy tia khúc xạ hợp với pháp tuyến của mặt phẳng phân cách của khối bán trụ góc khúc xạ 45o như hình vẽ.
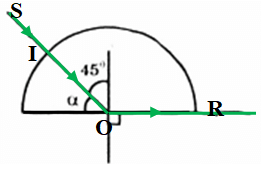
b) α = 45o
→ i = 90o – α = 45o → i = igh
→ r = 90o → Tia khúc xạ đi sát mặt phân cách của khối tròn như hình vẽ:
c) α = 30o
→ i = 90o – α = 60o → i > igh
→ Xảy ra phản xạ toàn phần, không có tia khúc xạ ra ngoài không khí. Đường đi của tia sáng được vẽ trên hình:

a/ \(\phi=N.BS\cos\left(\overrightarrow{B};\overrightarrow{n}\right)=200.10^{-4}.20.10^{-4}.\cos30^0=2\sqrt{3}.10^{-5}\left(T.m^2\right)\)
b/ \(E_c=\left|\frac{\Delta\phi}{\Delta t}\right|=\left|\frac{-2\sqrt{3}.10^{-5}}{0,01}\right|=2\sqrt{3}.10^{-3}\left(V\right)\)
\(Q=\frac{E_c^2}{R}t=\frac{\left(2\sqrt{3}.10^{-3}\right)^2}{10}.0,01=12.10^{-9}\left(J\right)\)
c/ \(I=\frac{E_c}{R+R'}=\frac{2\sqrt{3}.10^{-3}}{10+2}=\frac{\sqrt{3}.10^{-3}}{6}\left(A\right)\)
Check lại phần tính toán hộ mình nhé, nhiều số quá hơi nhức mắt :(
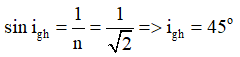
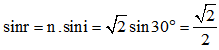
ta áp dụng vào công thức: F=\(BIl\)sinα, F cực tiểu khi sinα=0 hay α=00
vậy đáp án là A