
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a)\(\left(-a+\frac{2}{3}\right)\left(a+\frac{2}{3}\right)=\left(\frac{2}{3}-a\right)\left(\frac{2}{3}+a\right)=\left(\frac{2}{3}\right)^2-a^2=\frac{4}{9}-a^2\)
b)\(\left(x+5\right)\left(x^2-5x+25\right)=x^3+5^3=x^3+125\)
c)\(\left(1-x\right)\left(x^2+x+1\right)=1-x^3\)
d)\(\left(a^2-2a+3\right)\left(a^2+2a+3\right)=\left(a^2+3\right)^2-\left(2a\right)^2=\left(a^2+3\right)^2-4a^2\)
e)\(\left(x+3y\right)\left(9y^2-3xy+x^2\right)=x^3+\left(3y\right)^3=x^3+9y^3\)
f)\(2\left(x-\frac{1}{2}\right)\left(4x^2+2x+1\right)=\left(2x-1\right)\left(4x^2+2x+1\right)=\left(2x\right)^3-1=8x^3-1\)

Trả lời:
Bài 1:
a, \(9x^2-4=\left(3x\right)^2-2^2=\left(3x-2\right)\left(3x+2\right)\)
b, \(x^3+27=x^3+3^3=\left(x+3\right)\left(x^2-3x+9\right)\)
c, \(8-y^3=2^3-y^3=\left(2-y\right)\left(4+2y+y^2\right)\)
d, \(x^4-81=\left(x^2\right)^2-9^2=\left(x^2-9\right)\left(x^2+9\right)\)\(=\left(x^2-3^2\right)\left(x^2+9\right)=\left(x-3\right)\left(x+3\right)\left(x^2+9\right)\)
e, \(64x^3-1=\left(4x\right)^3-1^3=\left(4x-1\right)\left(16x^2+4x+1\right)\)
f, \(x^6+8y^3=\left(x^2\right)^3+\left(2y\right)^3=\left(x^2+2y\right)\left(x^4-2x^2y+4y^2\right)\)


a) ta có: \(\widehat{AMB}+\widehat{BMC}+\widehat{DMC}=180^o\Rightarrow\widehat{AMB}+\widehat{DMC}=90^0\)
đồng thời: \(\widehat{AMB}+\widehat{ABM}=90^0\)
\(\Rightarrow\widehat{DMC}=\widehat{ABM}\)
xét tam giác ABM và tam giác DMC có:
\(\widehat{MAB}=\widehat{MDC}=90^0\\ \widehat{ABM}=\widehat{DMC}\)
do đó tam giác ABM đồng dạng tam giác DMC(g-g)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{MD}{DC}\Rightarrow AB.DC=AM.MD\)
mà AM=MD, nên : \(AB.DC=AM.AM\)
b) vì tam giác ABM đồng dạng tam giác DMC nên:
\(\dfrac{BM}{MC}=\dfrac{AB}{MD}\:hay\:\dfrac{BM}{MC}=\dfrac{AB}{AM}\)
đồng thời: \(\widehat{MAB}=\widehat{MDC}=90^0\)
do đó tam giác ABM đồng dạng tam giác MBC(c-g-c)


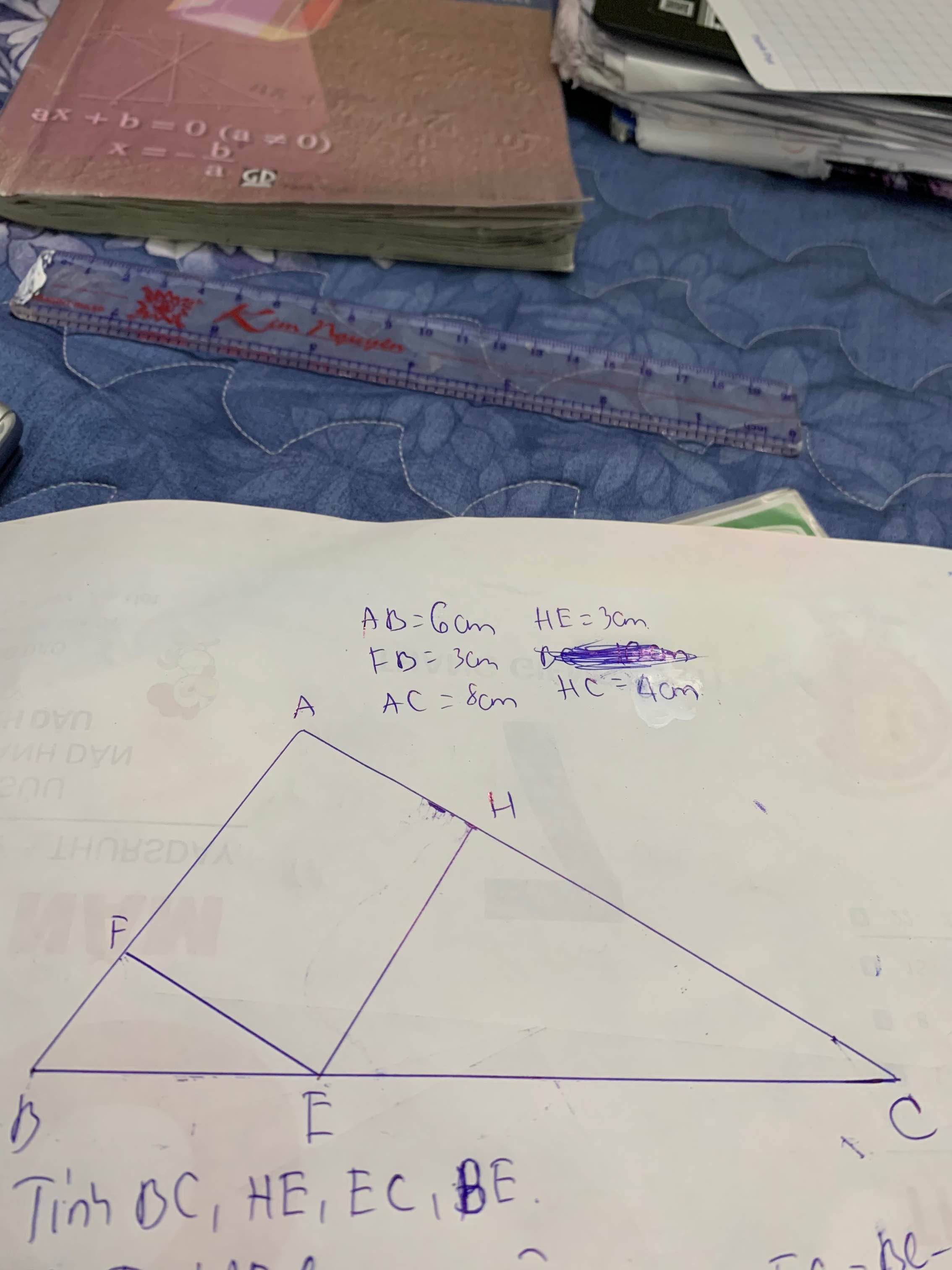


 mọi người giải giúp em với ạ em đang cần gấp lắm ạ
mọi người giải giúp em với ạ em đang cần gấp lắm ạ 
 đg cần gấp lúc 5h
đg cần gấp lúc 5h  lúc 5h
lúc 5h
