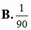Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Xét các số có 9 chữ số khác nhau:
- Có 9 cách chọn chữ số ở vị trí đầu tiên.
- Có 
cách chọn 8 chữ số tiếp theo
Do đó số các số có 9 chữ số khác nhau là: 
Xét các số thỏa mãn đề bài:
- Có 
cách chọn 4 chữ số lẻ.
- Đầu tiên ta xếp vị trí cho chữ số 0, do chữ số 0 không thể đứng đầu và cuối nên có 7 cách xếp.
- Tiếp theo ta có 
cách chọn và xếp hai chữ số lẻ đứng hai bên chữ số 0.
- Cuối cùng ta có 6! cách xếp 6 chữ số còn lại vào 6 vị trí còn lại.
Gọi A là biến cố đã cho, khi đó
Vậy xác suất cần tìm là 
Không gian mẫu: \(n\left(\Omega\right)=10!\)
Chọn 5 chữ số từ 6 chữ số còn lại (khác 0,3,6,8): có \(C_6^5\) cách
Hoán vị 6 chữ số (5 chữ số được chọn nói trên và số 8): \(6!\) cách
Tổng cộng: \(6!.C_6^5\) số
Xác suất: \(P=\dfrac{6!.C_6^5}{10!}=...\)
Chọn C
Có 2 bộ số {a;b;c} có tổng các chữ số bằng 5 là: {0;1;4}, {0;2;3}, mỗi bộ số có 3! hoán vị nên có tất cả 12 khả năng.
Do đó xác suất để người đó bấm máy một lần đúng số cần gọi là 1 12 .
Tham khảo:
Số phần tử của không gian mẫu là 
. Để người đó gọi đúng số điện thoại mà không phải thử quá hai lần ta có 2 trường hợp:
TH1: Người đó gọi đúng ở lần thứ nhất.
TH2: Người đó gọi đúng ở lần thứ hai. Gọi A1 người đó gọi đúng ở lần thứ nhất
Xác suất người đó gọi đúng là P(A1) = \(\dfrac{1}{10}\)
Xác suất người đó gọi không đúng là P(A1) = \(\dfrac{9}{10}\).
Gọi A2 là người đó gọi đúng ở lần thứ hai
Xác suất người đó gọi đúng là P(A2) = \(\dfrac{1}{9}\) .
Gọi A là người đó gọi đúng số điện thoại mà không phải thử quá hai lần, ta có 
(đpcm)
Giải
a, Có 6 chữ số khác nhau
Gọi số cần tìm là \(\overline{abcdef}\)
a có 5 cách chọn ( \(a\ne0\))
\(\overline{bcedf}\)có 5! cách chọn
=> Có tất cả 5.5! = 600 (số)
Vậy có 600 số có 6 chữ số khác nhau
b, Gọi số có 4 chữ số cần tìm là \(\overline{abcd}\)
Vì \(\overline{abcd}\) là số chẵn nên d \(\in\left(0,2,4\right)\)
TH1: d=0
\(\overline{abc}\) có \(A_5^3\) cách chọn => 60 cách chọn
TH2 : d=(2,4) -> có 2 cách chọn
a có 4 cách chọn ( a khác 0,d)
b có 4 cách chọn ( b khác a,d)
c có 3 cách chọn ( c khác a,b,d)
=> 4.4.3.2=96 số
Nên kết hợp hai trường hợp ta có 60+96=156 ( số)
Vậy có 156 số có 4 chữ số chẵn khác nhau
c, Gọi số có 3 chữ số khác nhau là \(\overline{abc}\)
TH1:
a = {4,5} -> có 2 cách
\(\overline{bc}\) có \(A_4^2\) cách chọn
=> Có 2.\(A_4^2\)=2.12=24 số
TH2: a=3 -> có 1 cách
b={1,2,4,5} -> có 4 cách
c có 4 cách ( c khác a,b)
=> 4.4=16 (số)
TH3: a=3 -> có 1 cách chọn
b=0-> có 1 cách chọn
c={1,2,4,5} -> có 4 cách chọn
=> có 4 số
Nên ta có 24+16+4=44( số)
Vậy có tất cả 44 số có 3 chữ số khác nhau lớn hơn 300