
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Đây có phải là toán lớp 8 nữa không vậy :)? Mình học toán nâng cao nhưng chưa bao giờ thấy dạng này :).
b1:
do x;y thuộc số nguyên N và x,y\(\ge\)2
=>\(-4xy+1< +7x-7y< 4xy+1\)
\(\Rightarrow4x^2y^2-4xy+1< 4x^2y^2+7x-7y< 4x^2y^2+4xy+1\)
\(\Rightarrow\left(2xy-1\right)^2< 4x^2y^2+7x-7y< \left(2xy+1\right)^2\)
mà \(4x^2y^2+7x-7y\) là số chính phương và 1<2xy-1<2xy-1 nên ta có:
\(4x^2y^2+7x-7y-\left(2xy\right)^2\Leftrightarrow x=y\)

ĐKXĐ: \(x\notin\left\{0;-9\right\}\)
Ta có: \(\dfrac{1}{x+9}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20x}{20x\left(x+9\right)}-\dfrac{20\left(x+9\right)}{20x\left(x+9\right)}=\dfrac{4x\left(x+9\right)+5x\left(x+9\right)}{20x\left(x+9\right)}\)
Suy ra: \(4x^2+36x+5x^2+45x=20x-20x-180\)
\(\Leftrightarrow9x^2+81x+180=0\)
\(\Leftrightarrow x^2+9x+20=0\)
\(\Leftrightarrow x^2+4x+5x+20=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(nhận\right)\\x=-5\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-4;-5}

\(\frac{x+2}{2019}+\frac{x+3}{2018}=\frac{x+4}{2017}+\frac{x}{2021}\)
\(\Leftrightarrow\frac{x+2}{2019}+1+\frac{x+3}{2018}+1=\frac{x+4}{2017}+1+\frac{x}{2021}+1\)
\(\Leftrightarrow\frac{x+2021}{2019}+\frac{x+2021}{2018}=\frac{x+2021}{2017}+\frac{x+2021}{2021}\)
\(\Leftrightarrow x+2021=0\)
\(\Leftrightarrow x=-2021\)

Hướng làm:
Thấy cả tử mẫu cộng lại đều bằng 2021 → Cộng thêm 1 rồi quy đồng với mỗi phân thức
\(\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\\ \Leftrightarrow\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\\ \Leftrightarrow\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}\right)=0\\ \Leftrightarrow x+2021=0\Leftrightarrow x=-2021\)
\(< =>\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\)
\(< =>\dfrac{x+2+2019}{2019}+\dfrac{x+3+2018}{2018}=\dfrac{x+4+2017}{2017}+\dfrac{x+2021}{2021}\)
\(< =>\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\)
\(< =>\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}=\right)=0\)
\(< =>x+2021=0< =>x=-2021\)
Vậy....

\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)

\(a,A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(=x-0,2-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(=\left(-0,2-2+2\right)+\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)\)
\(=-0,2\)
\(b,B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(=x^3-8y^3-x^3+8y^3-10\)
\(=-10\)
\(c,C=4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x-1\right)\left(x+1\right)-4x\)
\(=4\left(x^2+2x+1\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=13\)
a) \(A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(A=x-\dfrac{1}{5}-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(A=\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)-\left(\dfrac{1}{5}+2-2\right)\)
\(A=-\dfrac{1}{5}\)
Vậy: ...
b) \(B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(B=\left[x^3-\left(2y\right)^3\right]-\left[x^3-\left(2y\right)^3\right]-10\)
\(B=-10\)
Vậy: ...
c) \(4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x+1\right)\left(x-1\right)-4x\)
\(=4\left(x^2+2x+4\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=\left(4x^2+4x^2-8x^2\right)+\left(8x-4x-4x\right)+\left(4+1+8\right)\)
\(=13\)
Vậy:...

a: Xét tứ giác BFCE có
D là trung điểm của BC
D là trung điểm của FE
Do dó: BFCE là hình bình hành
b: Xét tứ giác ABFE có
AB//FE
AB=FE
Do đó: ABFE là hình bình hành
mà \(\widehat{FAB}=90^0\)
nên ABFE là hình chữ nhật

\(P=\frac{2bc-2016}{3c-2bc+2016}-\frac{2b}{3-2b+ab}+\frac{4032-3ac}{3ac-4032+2016a}\)
\(=\frac{2bc-abc}{3c-2bc+abc}-\frac{2b}{3-2b+ab}+\frac{2abc-3ac}{3ac-2abc+a^2bc}\)
\(=\frac{c\left(2b-ab\right)}{c\left(3-2b+ab\right)}-\frac{2b}{3-2b+ab}+\frac{ac\left(2b-3\right)}{ac\left(3-2b+ab\right)}\)
\(=\frac{2b-ab}{3-2b+ab}-\frac{2b}{3-2b+ab}+\frac{2b-3}{3-2b+ab}\)
\(=\frac{2b-ab-2b+2b-3}{3-2b+ab}=\frac{2b-ab-3}{-\left(2b-ab-3\right)}=-1\)
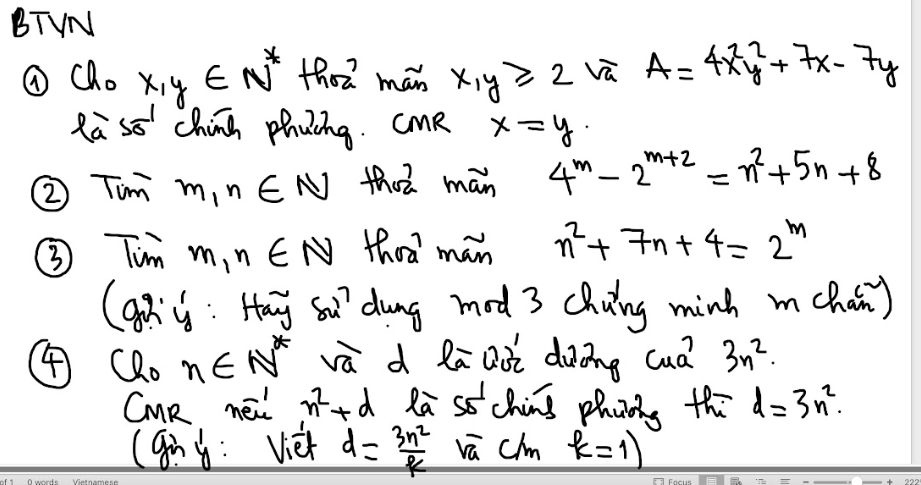





a, Vì D,M là trung điểm AB,AC nên DM là đtb tg ABC
Do đó \(DM=\dfrac{1}{2}BC=\dfrac{7}{2}\left(cm\right)\) và DM//BC
anh ơi có hình ko ạ, em ko bt vẽ hình