Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Mình cảm ơn ạ
Bài 4 : 8^8 + 2^20 = 2^3)^8 + 2^20 = 2^24 + 2^20 = 2^19 x 32 + 2^19 x 2 = 2^19 x (32 + 2) = 2^19 x 34 chia hết cho 17
Bài 5 : m + 4n \(⋮\)13 khi 10m + n \(⋮\)13
4 x (10m + n) = 40m + 4 n = 39m + m + 4n \(⋮\)13 (vì 39m \(⋮\)13 nên m + 4n \(⋮\)13)
Bài 6 : (x + y) (x - y) = 2002 = x . (x - y) + y . (x - y) = x . x - x . y + y . x - y . y = x^2 - x .y + y . x - y^2 = x^2 - y^2 = 2002 => không tồn tại hai số x và y
Bài 7 mk chịu
Bài 8 : nếu ab + cd \(⋮\)11 thì abcd \(⋮\)11
abcd = ab00 + cd = ab x 100 + cd = ab x 99 + ab + cd => nếu ab + cd chia hết cho 11 thì abcd chia hết cho 11
Bài 9 : abc và deg : 11 dư 5 abcdeg \(⋮\)11
cho abc = 11m + 5 deg = 11n + 5
abcdeg = abc000 + deg = abc x 1000 + deg = (11m + 5) x 1000 + 11n + 5 = 11m x 1000 + 5000 + 11n + 5 = 11m + 11n + 5005 = 11(m + n) + 5005 (vì 11(m + n) chia hết cho 11 và 5005 chia hết cho 11 nên abcdeg chia hết cho 11)
Bài 10 : abc - deg chia hết cho 13 abcdeg chia hết cho 13 (bạn chứng minh như cách trên)
nếu abc và deg chia hết cho 13 thì abcdeg = abc000 + deg = 13m x 1000 + 13n \(⋮\)13
nếu abc và deg không chia hết cho 13 thì abc = 13m + x và deg = 13n + x ( vì nếu hai số dư khác nhau thì hiệu hai số sẽ là 13k + (x - y)
abcdeg = abc000 + deg = (13m + x) 1000 + 13n + x = 13m + 13n + x00x = 13(m + n) + x . 1001 = 13(m + n) + x . 13 . 77 \(⋮\)13
Bài 11 : abc chia hết cho 7 thì 2a + 3b + c chia hết cho 7
abc = a00 + b0 + c = a . 100 + b . 10 + c = a . 2 + a . 98 + b . 7 + b . 3 + c = 98a + 7b + (2a + 3b + c) \(⋮\)7 mà 98a và 7b chia hết cho 7 nên 2a + 3b + c chia hết cho 7
Bài 12 abc chia hết cho 4 thì bc chia hết cho 4 mà b là số chẵn nên b0 chia hết cho 4 , vậy c chia hết cho 4
bac chia hết cho 4 khi ac chia hết cho 4 mà c chia hết cho 4 mà a là số chẵn nên a0 chia hết cho 4 => ac chia hết cho 4
Bài 13 : a - b = 4 khi a = b + 4
7a5b1 chia hết cho 3 khi 7 + a + 5 + b + 1 chia hết cho 3 = 13 + a + b chia hết cho 3 a + b có thể bằng : 2 ; 5 ; 8
a có thể bằng : 6
b có thể bằng : 2
giải giúp mình với, mình cần gấp, ai. đúng thì mình tick nha ! Thanks
Trả lời:
\(\frac{5}{1.6}+\frac{5}{6.11}+...+\frac{5}{\left(5x+1\right)\left(5x+6\right)}=\frac{2005}{2006}\)
\(\Rightarrow1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+...+\frac{1}{5x+1}-\frac{1}{5x+6}=\frac{2005}{2006}\)
\(\Rightarrow1-\frac{1}{5x+6}=\frac{2005}{2006}\)
\(\Rightarrow\frac{1}{5x+6}=1-\frac{2005}{2006}\)
\(\Rightarrow\frac{1}{5x+6}=\frac{1}{2006}\)
\(\Rightarrow5x+6=2006\)
\(\Rightarrow5x=2000\)
\(\Rightarrow x=400\)
Vậy x = 400
Trả lời:
\(\frac{x}{2008}-\frac{1}{10}-\frac{1}{15}-\frac{1}{21}-...-\frac{1}{120}=\frac{5}{8}\)
\(\Rightarrow\frac{x}{2008}-\left(\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{120}\right)=\frac{5}{8}\)\(\frac{5}{8}\)
Đặt \(A=\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{120}\), ta được : \(\frac{x}{2008}-A=\frac{5}{8}\) (*)
\(\Rightarrow A=\frac{2}{20}+\frac{2}{30}+\frac{2}{42}+...+\frac{2}{240}\)
\(\Rightarrow A=2\left(\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+...+\frac{1}{240}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{15.16}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{15}-\frac{1}{16}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4}-\frac{1}{16}\right)=2.\frac{3}{16}=\frac{3}{8}\)
Thay A vào (*) , ta có:
\(\frac{x}{2008}-\frac{3}{8}=\frac{5}{8}\)
\(\Rightarrow\frac{x}{2008}=1\)
\(\Rightarrow x=2008\)
Vậy x = 2008
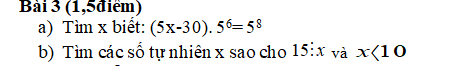
giải chi tiết giúp mik ạ
a: =11-11=0
c: =23x100=2300