HH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
1
4 tháng 1 2024
a: Xét ΔMQP có
H,I lần lượt là trung điểm của MQ,MP
=>HI là đường trung bình của ΔMQP
=>HI//QP và HI=QP/2
Xét ΔPMN có
I,K lần lượt là trung điểm của PM,PN
=>IK là đường trung bình của ΔPMN
=>IK//MN và \(IK=\dfrac{MN}{2}\)
b: H,I,K thẳng hàng
mà HI//PQ và IK//MN
nên HI//MN
Ta có: HI//MN
HI//PQ
Do đó: MN//PQ
NH
1
21 tháng 8 2019
Trả lời nhiều vào :)
Nhưng câu trả lời phải mang tính thuyết phục và có lí.
22 tháng 11 2021
\(a,=\left(2a-1\right)\left(2a+1\right)\\ b,=\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\\ c,=\left(16-3x\right)\left(16+3x\right)\\ d,Sửa:-36x^2+24x-4=-4\left(9x^2-6x+1\right)=-4\left(3x-1\right)^2\)
NT
2
10 tháng 8 2018
7x( y - 4 )2 - ( 4-y )3
= 7x ( 4 - y )2 ( 4-y )3
= ( 4 - y )2 [ 7x - ( 4 - y ) ]
= ( 4 - y )2 ( 7x + 4 - y )
học tốt!
10 tháng 8 2018
\(7x\left(y-4\right)^2-\left(4-y\right)^3=7x\left(4-y\right)^2-\left(4-y\right)^3\)
\(=\left(4-y\right)^2.\left[7x-\left(4-y\right)\right]\)
\(=\left(4-y\right)^2.\left(7x-4+y\right)\)
Chúc bạn học tốt.
17 tháng 7 2021
Ta có: \(\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+9\left(x+1\right)^2=15\)
\(\Leftrightarrow x^3-9x^2+27x-27-x^3+27+9\left(x^2+2x+1\right)=15\)
\(\Leftrightarrow-9x^2+27x+9x^2+18x+9=15\)
\(\Leftrightarrow45x=6\)
hay \(x=\dfrac{2}{15}\)
1 tháng 11 2021
Câu 20:
Ta có: \(\widehat{A}-\widehat{B}=40^0\Rightarrow\widehat{B}=\widehat{A}-40^0\)
\(\widehat{A}=2\widehat{C}\Rightarrow\widehat{C}=\frac{\widehat{A}}{2}\)
Vì AB//CD (gt) \(\Rightarrow\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)\(\Rightarrow\widehat{D}=180^0-\widehat{A}\)
Tứ giác ABCD \(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\Rightarrow\widehat{A}+\left(\widehat{A}-40^0\right)+\frac{\widehat{A}}{2}+\left(180^0-\widehat{A}\right)=360^0\)
Và đến đây bạn dễ dàng tìm được góc A và từ đó suy ra được góc D.
1 tháng 11 2021
Câu 29: Ta có:
\(\hept{\begin{cases}xy+x+y=3\\yz+y+z=8\\xz+x+z=15\end{cases}}\Leftrightarrow\hept{\begin{cases}xy+x+y+1=4\\yz+y+z+1=9\\xz+x+z+1=16\end{cases}\Leftrightarrow}\hept{\begin{cases}x\left(y+1\right)+\left(y+1\right)=4\\y\left(z+1\right)+\left(z+1\right)=9\\x\left(z+1\right)+\left(z+1\right)=16\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)\left(y+1\right)=4\\\left(y+1\right)\left(z+1\right)=9\\\left(z+1\right)\left(x+1\right)=16\end{cases}}\)
Đặt \(\hept{\begin{cases}x+1=a\\y+1=b\\z+1=c\end{cases}}\)với a,b,c > 1, khi đó ta có
\(\hept{\begin{cases}ab=4\\bc=9\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}abbc=4.9\\c=\frac{9}{b}\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}16b^2=36\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b^2=\frac{36}{16}=\frac{9}{4}\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b=\frac{3}{2}\\c=\frac{9}{\frac{3}{2}}=6\\a=\frac{16}{6}=\frac{8}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=a-1=\frac{8}{3}-1=\frac{5}{3}\\y=b-1=\frac{3}{2}-1=\frac{1}{2}\\z=c-1=6-1=5\end{cases}}\)
Vậy \(P=x+y+z=\frac{5}{3}+\frac{1}{2}+5=\frac{10+3+30}{6}=\frac{43}{6}\)
11 tháng 2 2022
\(\Rightarrow12+20x-60=45x-15\Leftrightarrow25x=-33\Leftrightarrow x=-\dfrac{33}{25}\)
23 tháng 11 2022
Bạn đổi I thành M nha
Gọi I là trung điểm của KC
Xét ΔKHC có M,I lần lượt là trung điểm của KH,KC
nên MI là đường trung bình
=>MI//HC
=>MI vuông góc với AH
Xét ΔAHI có
IM,HK là các đường cao
IM cắt HK tại M
Do đó: M là trực tâm
=>AM vuông góc với HI
Xét ΔBKC có
CH/CB=CI/CK
nên HI//BK
=>AM vuông góc với BK
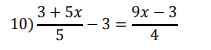
các GP ;CTV học 24 xem giùm mk vs
Chảo bạn. Bạn cố gắng trình bày sạch đẹp, công thức cẩn thận thì khả năng được tick sẽ cao hơn nhé.