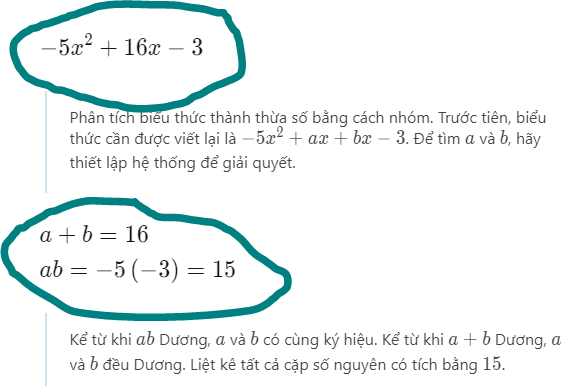Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=x^2+x+3x+3=x\left(x+1\right)+3\left(x+1\right)=\left(x+1\right)\left(x+3\right)\)

\(=-5x^2+15x+x-3=-5x\left(x-3\right)+\left(x-3\right)=\left(1-5x\right)\left(x-3\right)\)

\(=x\left(\frac{x^2}{4}+x+1\right)=x\left(\frac{x}{2}+1\right)^2\)

\(x^3+9x^2+26x+24\)
\(=x^3+3x^2+6x^2+18x+8x+24\)
\(=\left(x^3+3x^2\right)+\left(6x^2+18x\right)+\left(8x+24\right)\)
\(=x^2\left(x+3\right)+6x\left(x+3\right)+8\left(x+3\right)\)
\(=\left(x+3\right)\left(x^2+6x+8\right)\)
\(=\left(x+3\right)\left(x^2+2x+4x+8\right)\)
\(=\left(x+3\right)\left[\left(x^2+2x\right)+\left(4x+8\right)\right]\)
\(=\left(x+3\right)\left[x\left(x+2\right)+4\left(x+2\right)\right]\)
\(=\left(x+3\right)\left(x+2\right)\left(x+4\right)\)

\(15^3+29x^2-8x-12=15x^3+30x^2-x^2-2x-6x-12\)
= \(15x^2.\left(x+2\right)-x.\left(x+2\right)-6.\left(x+2\right)\)= \(\left(x+2\right).\left(15x^2-x-6\right)\)
= \(\left(x+2\right).\left(15x^2-10x+9x-6\right)\)= \(\left(x+2\right).\left(3x-2\right).\left(5x+3\right)\)
\(x^3+9x^2+26x+24=x^3+3x^2+6x^2+18x+8x+24\)\(=x.^2\left(x+3\right)+6x.\left(x+3\right)+8.\left(x+3\right)\)\(=\left(x+3\right).\left(x^2+6x+8\right)\)\(\left(x+3\right).\left(x^2+2x+4x+8\right)=\left(x+2\right).\left(x+3\right).\left(x+4\right)\)

Ta có : 15x3 + 29x2 - 8x - 12
= 15x3 + 30x2 - x2 - 8x - 12
= 15x(x + 2) - (8x + 16) - (x2 - 4)
= 15x(x + 2) - 8(x + 2) - (x - 2)(x + 2)
= (x + 2)(15x - 8 - x + 2)
= (x + 2) (14x - 6)
click zô nha >_<

a) (2x - 1)2 - (x + 3)2
= (2x - 1 - x - 3).(2x - 1 + x + 3)
= (x - 4).(3x + 2)
b) x2.(x - 3) + 12 - 4x
= x2.(x - 3) - 4x + 12
= x2.(x - 3) - 4.(x - 3)
= (x - 3).(x2 - 4)
= (x - 3).(x - 2).(x + 2)
Áp dụng HĐT:
a2 - b2 = (a - b)(a + b)
\(\left(2x-1\right)^2-\left(x+3\right)^2\)
\(=\left(2x-1-x-3\right)\left(2x-1+x+3\right)\)
\(=\left(x-4\right)\left(3x+2\right)\)

\(x^8+3x^4+4\)
\(=\left(x^8-x^6+2x^4\right)+\left(x^6-x^4+2x^2\right)+\left(2x^4-2x^2+4\right)\)
\(=x^4\left(x^4-x^2+2\right)+x^2\left(x^4-x^2+2\right)+2\left(x^4-x^2+2\right)\)
\(=\left(x^4+x^2+2\right)\left(x^4-x^2+2\right)\)
\(4x^4+4x^3+5x^2+2x+1\)
\(=\left(4x^4+2x^3+2x^2\right)+\left(2x^3+x^2+x\right)+\left(2x^2+x+1\right)\)
\(=2x^2\left(2x^2+x+1\right)+x\left(2x^2+x+1\right)+\left(2x^2+x+1\right)\)
\(=\left(2x^2+x+1\right)^2\)