Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=\left(\dfrac{19}{6}-\dfrac{2}{5}\right):\left(\dfrac{29}{6}+\dfrac{7}{10}\right)\)
\(=\dfrac{19\cdot5-2\cdot6}{30}:\dfrac{290+42}{30}=\dfrac{83}{332}=\dfrac{1}{4}\)
b: \(=\dfrac{\left(\dfrac{102}{25}-\dfrac{2}{25}\right)\cdot\dfrac{17}{4}}{\left(6+\dfrac{5}{9}-3-\dfrac{1}{4}\right)\cdot\dfrac{16}{7}}\)
\(=\dfrac{4\cdot\dfrac{17}{4}}{\dfrac{16}{7}\cdot\dfrac{119}{36}}=\dfrac{17}{\dfrac{68}{9}}=17\cdot\dfrac{9}{68}=\dfrac{9}{4}\)
c: \(=\left(\dfrac{120}{60}-\dfrac{15}{60}+\dfrac{20}{60}-\dfrac{36}{60}\right):\left(\dfrac{45}{15}-\dfrac{3}{15}-\dfrac{25}{15}\right)\)
\(=\dfrac{89}{60}:\dfrac{17}{15}=\dfrac{89}{60}\cdot\dfrac{15}{17}=\dfrac{89}{68}\)

a: (x+1/2)(2/3-2x)=0
=>x+1/2=0 hoặc 2/3-2x=0
=>x=-1/2 hoặc x=1/3
b: 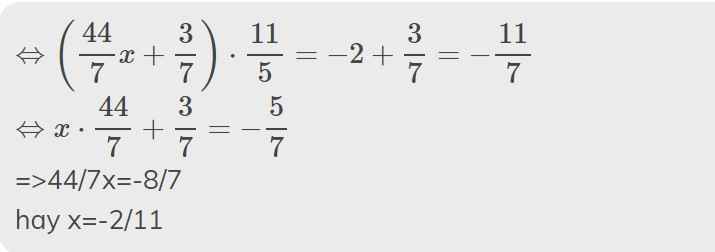
c: \(\Leftrightarrow x\cdot\left(\dfrac{13}{4}-\dfrac{7}{6}\right)=\dfrac{5}{12}+\dfrac{5}{3}=\dfrac{5}{12}+\dfrac{20}{12}=\dfrac{25}{12}\)
\(\Leftrightarrow x=\dfrac{25}{12}:\dfrac{39-14}{12}=\dfrac{25}{25}=1\)

Bài 1:
a: \(A=\dfrac{1\left(\dfrac{1}{13}-\dfrac{1}{17}-\dfrac{1}{23}\right)}{2\left(\dfrac{1}{13}-\dfrac{1}{17}-\dfrac{1}{23}\right)}\cdot\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{7}{6}-\dfrac{7}{8}+\dfrac{7}{10}}+\dfrac{6}{7}\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{7}+\dfrac{6}{7}=\dfrac{1}{7}+\dfrac{6}{7}=1\)
b: \(B=2000:\left[\dfrac{\dfrac{2}{5}-\dfrac{2}{9}+\dfrac{2}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}\cdot\dfrac{-\dfrac{7}{6}+\dfrac{7}{8}-\dfrac{7}{10}}{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}\right]\)
\(=2000:\left[\dfrac{2}{7}\cdot\dfrac{-7}{2}\right]=-2000\)
c: \(C=10101\cdot\left(\dfrac{5}{111111}+\dfrac{1}{111111}-\dfrac{4}{111111}\right)\)
\(=10101\cdot\dfrac{2}{111111}=\dfrac{2}{11}\)

Các câu dễ tự làm nha:
\(D=\dfrac{1}{100.99}-\dfrac{1}{99.98}-\dfrac{1}{98.97}-...-\dfrac{1}{3.2}-\dfrac{1}{2.1}\)
\(D=\dfrac{1}{99}-\dfrac{1}{100}-\dfrac{1}{99}+\dfrac{1}{98}-\dfrac{1}{98}+\dfrac{1}{97}-...-\dfrac{1}{2}+\dfrac{1}{3}-1+\dfrac{1}{2}\)\(D=-\dfrac{1}{100}-1\)

1.a) Dễ nhận thấy đề toán chỉ giải được khi đề là tìm x,y. Còn nếu là tìm x ta nhận thấy ngay vô nghiệm. Do đó: Sửa đề: \(\left|x-3\right|+\left|2-y\right|=0\)
\(\Leftrightarrow\left|x-3\right|=\left|2-y\right|=0\)
\(\left|x-3\right|=0\Rightarrow\left\{{}\begin{matrix}x-3=0\\-\left(x-3\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\) (1)
\(\left|2-y\right|=0\Rightarrow\left\{{}\begin{matrix}2-y=0\\-\left(2-y\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\y=-2\end{matrix}\right.\) (2)
Từ (1) và (2) có: \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x_1=3\\x_2=-3\end{matrix}\right.\\\left\{{}\begin{matrix}y_1=2\\y_2=-2\end{matrix}\right.\end{matrix}\right.\)

a: \(\Leftrightarrow\dfrac{8}{5}+\dfrac{2}{5}\cdot x=\dfrac{16}{5}\)
=>2/5x=8/5
=>x=4
b: \(\Leftrightarrow\left(\dfrac{1}{24}-\dfrac{1}{25}+\dfrac{1}{25}-\dfrac{1}{26}+...+\dfrac{1}{39}-\dfrac{1}{40}\right)\cdot120+\dfrac{1}{3}x=-4\)
\(\Leftrightarrow x\cdot\dfrac{1}{3}+2=-4\)
=>1/3x=-6
=>x=-18
c: =>2|x-1/3|=0,24-4/5=-0,56<0

7) \(\dfrac{-5}{17}+\dfrac{3}{17}\le\dfrac{x}{17}\le\dfrac{13}{17}+\dfrac{-11}{17}\)
\(\Rightarrow\dfrac{-2}{17}\le\dfrac{x}{17}\le\dfrac{2}{17}\)
\(\Rightarrow-2\le x\le2\)
\(\Rightarrow x\in\left\{-2;-1;0;1;2\right\}\)
8) \(\dfrac{2}{3}\left(\dfrac{1}{2}+\dfrac{3}{4}-\dfrac{1}{3}\right)\le\dfrac{x}{18}\le\dfrac{7}{3}\left(\dfrac{1}{2}-\dfrac{1}{6}\right)\)
\(\Rightarrow\dfrac{2}{3}\left(\dfrac{6}{12}+\dfrac{9}{12}-\dfrac{4}{12}\right)\le\dfrac{x}{18}\le\dfrac{7}{3}\left(\dfrac{6}{12}-\dfrac{2}{12}\right)\)
\(\Rightarrow\dfrac{2}{3}\cdot\dfrac{11}{12}\le\dfrac{x}{18}\le\dfrac{7}{3}\cdot\dfrac{4}{12}\)
\(\Rightarrow\dfrac{22}{36}\le\dfrac{x}{18}\le\dfrac{28}{36}\)
\(\Rightarrow\dfrac{11}{18}\le\dfrac{x}{18}\le\dfrac{14}{18}\)
\(\Rightarrow x\in\left\{11;12;13;14\right\}\)
8) \(\dfrac{2}{3}\left(\dfrac{1}{2}+\dfrac{3}{4}-\dfrac{1}{3}\right)\le\dfrac{x}{18}\le\dfrac{7}{3}\left(\dfrac{1}{2}-\dfrac{1}{6}\right)\\ \dfrac{2}{3}\left(\dfrac{6}{12}+\dfrac{9}{12}-\dfrac{4}{12}\right)\le\dfrac{x}{18}\le\dfrac{7}{3}\left(\dfrac{3}{6}-\dfrac{1}{6}\right)\\ \dfrac{2}{3}.\dfrac{11}{12}\le\dfrac{x}{18}\le\dfrac{7}{3}.\dfrac{2}{6}\\ \dfrac{11}{18}\le\dfrac{x}{18}\le\dfrac{14}{18}\\ \Rightarrow11\le x\le14\\ \Rightarrow x\in\left\{11;12;13;14\right\}\)

a)
Ta thấy:
\(\dfrac{1}{6}< \dfrac{1}{5}\)
\(\dfrac{1}{7}< \dfrac{1}{5}\)
\(\dfrac{1}{8}< \dfrac{1}{5}\)
\(\dfrac{1}{9}< \dfrac{1}{5}\)
\(\dfrac{1}{11}< \dfrac{1}{10}\)
\(\dfrac{1}{12}< \dfrac{1}{10}\)
\(\dfrac{1}{13}< \dfrac{1}{10}\)
...
\(\dfrac{1}{17}< \dfrac{1}{10}\)
\(\Rightarrow\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}< 5\cdot\dfrac{1}{5}+8\cdot\dfrac{1}{10}=1+\dfrac{4}{5}=\dfrac{9}{5}< 2\)
Vậy \(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}< 2\)
b)
Ta thấy:
\(\dfrac{1}{101}>\dfrac{1}{300}\)
\(\dfrac{1}{102}>\dfrac{1}{300}\)
\(\dfrac{1}{103}>\dfrac{1}{300}\)
...
\(\dfrac{1}{299}>\dfrac{1}{300}\)
\(\Rightarrow\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{300}>200\cdot\dfrac{1}{300}=\dfrac{2}{3}\)
Vậy \(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{300}>\dfrac{2}{3}\)
Không tính thì sao mà làm được :)
a)
\(2020-\dfrac{1}{3^2}-\dfrac{1}{4^2}-...-\dfrac{1}{2019^2}\)
\(=3+\left(1-\dfrac{1}{3^2}\right)+\left(1-\dfrac{1}{4^2}\right)+....+\left(1-\dfrac{1}{2019^2}\right)\)
\(=3+\left(\dfrac{3^2-1}{3^2}+\dfrac{4^2-1}{4^2}+...+\dfrac{2019^2-1}{2019^2}\right)\)
\(=3+\left(\dfrac{2\cdot4}{3^2}+\dfrac{3\cdot5}{4^2}+\dfrac{4\cdot6}{5^2}+\dfrac{5\cdot7}{6^2}+...+\dfrac{2018\cdot2020}{2019^2}\right)\)
\(=3+\dfrac{\left(2\cdot3\cdot4\cdot....\cdot2018\right)}{3\cdot4\cdot5\cdot6...\cdot2019}\cdot\dfrac{\left(3\cdot4\cdot5\cdot....\cdot2020\right)}{3\cdot4\cdot5\cdot6\cdot....\cdot2019}=3+\dfrac{2\cdot2020}{2019}\)
\(=\dfrac{10097}{2019}\)
Có: \(\dfrac{1}{k^2}=\dfrac{1}{k.k}< \dfrac{1}{\left(k-1\right)k}\left(k\in\text{ℕ},k>0\right)\)
\(\Rightarrow A=2020-\dfrac{1}{3^2}-\dfrac{1}{4^2}-\dfrac{1}{5^2}-...-\dfrac{1}{2019^2}\)
\(A=2020-\left(\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+...+\dfrac{1}{2019^2}\right)\)
\(>2020-\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{2018.2019}\right)\)
Có: \(\dfrac{1}{k-1}-\dfrac{1}{k}=\dfrac{1}{k\left(k-1\right)}\left(k\in\text{ℕ},k>0\right)\)
\(\Rightarrow A>2020-\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-...+\dfrac{1}{2018}-\dfrac{1}{2019}\right)\)
\(A>2020-\dfrac{1}{2}+\dfrac{1}{2019}\)>2,2
Có: \(B=\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{17}\)
\(B=\dfrac{1}{5}+\left(\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}\right)\)\(< \dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{6}+...+\dfrac{1}{6}\)
\(=\dfrac{1}{5}+\dfrac{1}{6}.12=2+\dfrac{1}{5}=2,2\)
Vậy A>B.