Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CM bđt theo phương pháp tương đương:
Ta có: \(\sqrt{14}-\sqrt{13}< 2\sqrt{3}-\sqrt{11}\)
<=> \(\sqrt{14}+\sqrt{11}< \sqrt{12}+\sqrt{13}\)
<=> \(14+11+2\sqrt{14.11}< 12+13+2\sqrt{12.13}\)
<=> \(\sqrt{14.11}< \sqrt{12.13}\)
<=> \(14.11< 12.13\)
Ta có: 14.11 = 12.11 + 2.11 = 12.13 - 2.12 + 2.11 = 12.13 - 2(12 - 11) = 12.13 - 2 < 12.13
=> 14.11 < 12.13 (luôn đúng)
=> \(\sqrt{14}-\sqrt{13}< 2\sqrt{3}-\sqrt{11}\)(luôn đúng)

\(\sqrt{2}\left(\sqrt{3}+1\right)\)
\(=\sqrt{6}+\sqrt{2}\)
Ta có: \(\left(\sqrt{6}+\sqrt{2}\right)^2=8+4\sqrt{3}\)
Và: \(\left(\sqrt{3}+2\right)^2=7+4\sqrt{3}\)
Ta thấy: \(8+4\sqrt{3}>7+4\sqrt{3}\)
Hay: \(\sqrt{2}\left(\sqrt{3}+1\right)>\sqrt{3}+2\) (đpcm)

giả sử: \(x^{17}+y^{17}=19^{17}\) và \(1\le x\le y\le19\)
Ta có: \(19^{17}\ge\left(y+1\right)^{17}\)
\(\Rightarrow19^{17}>y^{17}+17y^{16}\)
Vậy x>17, chỉ có thể x=y=18
Thử lại, x=y=18 không thoả
Vậy pt đã cho không có nghiệm nguyên

Mình học lớp 6 nên chẳng may có gì sai bạn(chị anh) sửa giúp em nhé:
Ta có:
\(\left(\sqrt{n+a}+\sqrt{n-a}\right)^2< \left(2\sqrt{n}\right)^2\) (bình phương cả 2 vế)
=> \(2n+2\sqrt{n^2-a^2}< 4n\)
=>\(2\sqrt{n^2-a^2}< 2n\)
=>\(\sqrt{n^2-a^2}< n\)
=>n2 - a2 < n2 (bình phương cả 2 vế)
Vì |a|>0
=>a2 > 0
=> n2-a2 < n2
Vậy \(\sqrt{n+a}+\sqrt{n-a}< 2\sqrt{n}\)
câu b làm tương tự nhé:

Tham khảo
https://olm.vn/hoi-dap/tim-kiem?id=638956&subject=1&q=++++++++++CMR+(n4-1)+chia+het+cho+8,+v%E1%BB%9Bi+m%E1%BB%8Di+n+l%E1%BA%BB+b%E1%BA%A5t+k%C3%AC+++++++++

\(8^2=64=32+2\sqrt{16^2}\)
\(\left(\sqrt{15}+\sqrt{17}\right)^2=32+2\sqrt{15.17}=32+2\sqrt{\left(16-1\right)\left(16+1\right)}\)
\(=32+2\sqrt{16^2-1}\)
\(< =>8^2>\left(\sqrt{15}+\sqrt{17}\right)^2\)
\(8>\sqrt{15}+\sqrt{17}\)
\(\left(\sqrt{2019}+\sqrt{2021}\right)^2=4040+2\sqrt{2019.2021}\)
\(=4040+2\sqrt{\left(2020-1\right)\left(2020+1\right)}=4040+2\sqrt{2020^2-1}\)
\(\left(2\sqrt{2020}\right)^2=8080=4040+2\sqrt{2020^2}\)
\(< =>\sqrt{2019}+\sqrt{2021}< 2\sqrt{2020}\)
mik chọn điền
<
mik lười chép ại đề bài



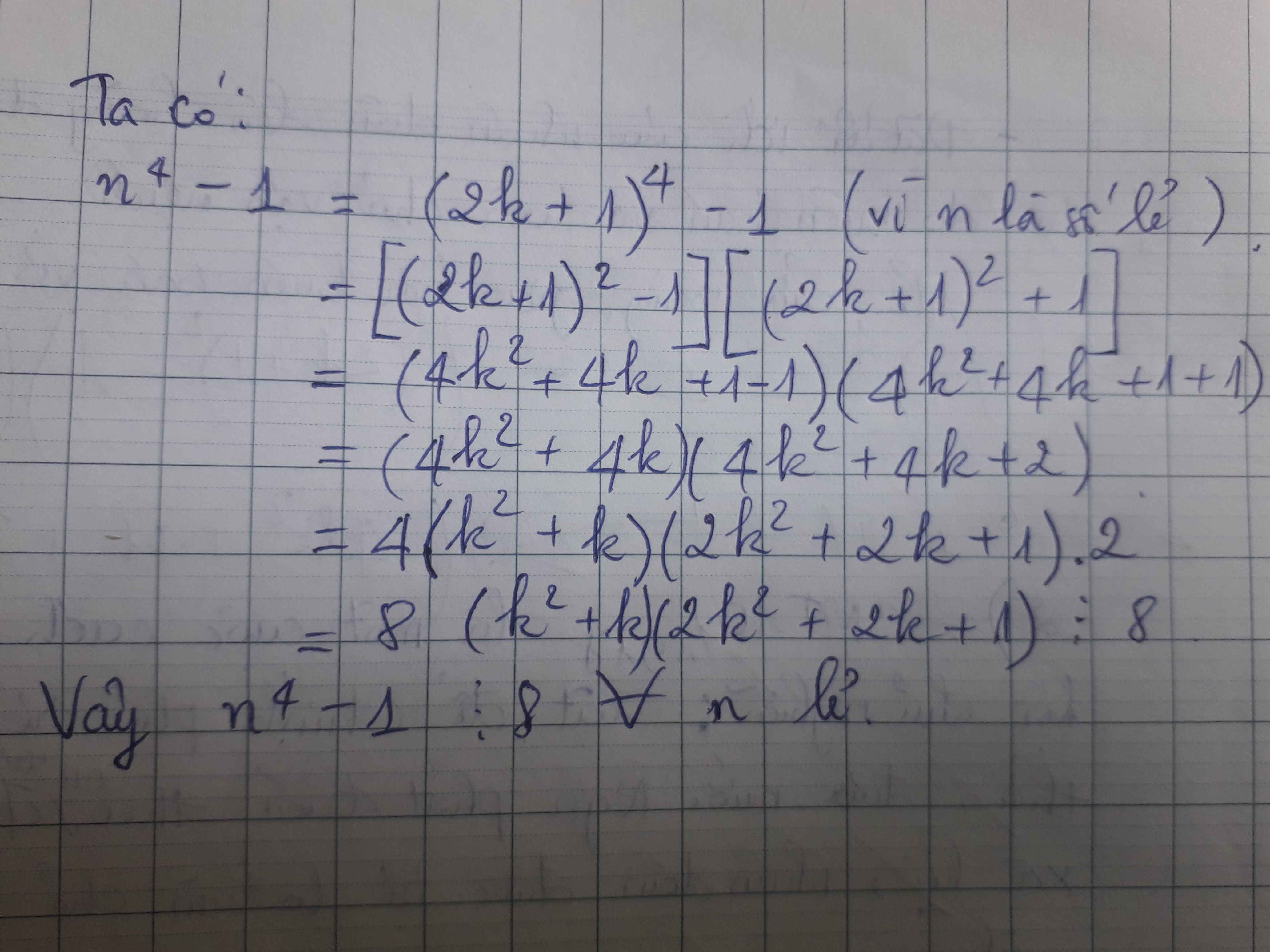
=????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????