Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
. Gọi M là giao điểm của AD với OI, N là giao điểm của AE với O’I 
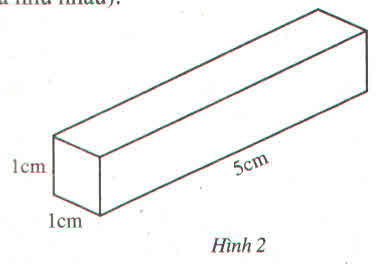
Gọi x(cm) là chiều dài của sợi dây.
Vì thể tích của khối vàng không thay đổi nên diện tích mặt cắt ngang và chiều dài hình hộp chữ nhật là hai đại lượng tỉ lệ nghịch
Ta có: \(0,01x=1.5\Rightarrow x=\dfrac{1,5}{0,01}=500\left(cm\right)\)
Vậy mặt cắt ngang là hình vuông có cạnh 1mm thì chiều dài sợi dây là 500cm.
Gọi x(cm) là chiều dài của sợi dây.
Vì thể tích của khối vàng không thay đổi nên diện tích mặt cắt ngang và chiều dài hình hộp chữ nhật là hai đại lượng tỉ lệ nghịch
Ta có: 0,01x=1.5⇒x=1,50,01=500(cm)0,01x=1.5⇒x=1,50,01=500(cm)
Vậy mặt cắt ngang là hình vuông có cạnh 1mm thì chiều dài sợi dây là 500cm.
A (0,5; 2) B (2;2) C (2;0)
D (0,5; 0) P (-3;3) Q (-1;1)
R(-3;1)
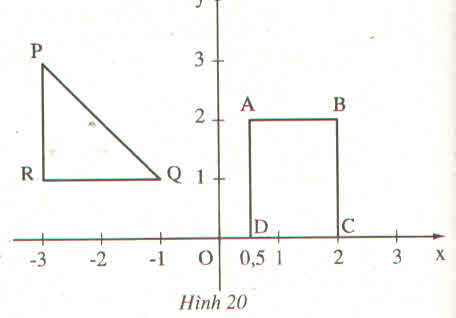
- A(0,5 ; 2); B(2 ; 2); C(2 ; 0); D(0,5 ; 0)
- P(-3 ; 3) ; Q(-1 ; 1) ; R(-3 ; 1)
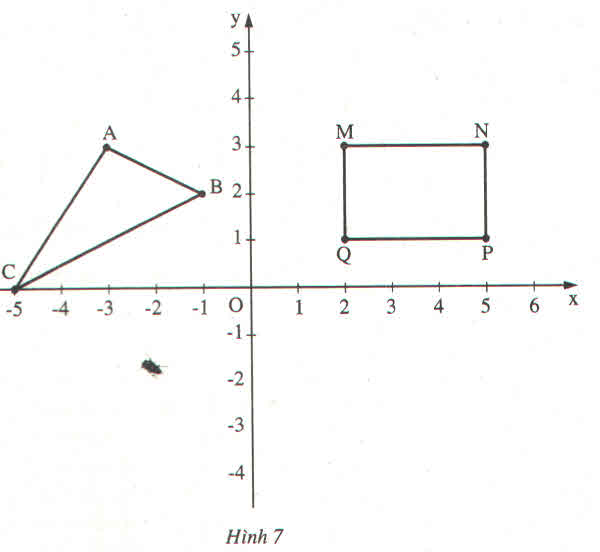
A( -3; 3 )
B ( -1; 2 )
C ( -5; 0 )
M ( 2; 3 )
N ( 5; 3 )
Q ( 2; 1 )
P (5; 1 )
đúng rồi
- Kẻ AH⊥aAH⊥a kéo dài, HA cắt b tại B.
- Kẻ AK⊥bAK⊥b kéo dài KA cắt a tại C.
- Kẻ AI⊥BCAI⊥BC, đường thẳng AI đi qua O.
Vì trong ∆OBC có 2 đường cao BH và CK cắt nhau tại A nên A là trực tâm của ∆OBC.
OA là đường cao thứ 3 nên OA⊥BCOA⊥BC
AI⊥BCAI⊥BC nên đường thẳng OA và đường thẳng AI trùng nhau hay đường thẳng AI đi qua O.
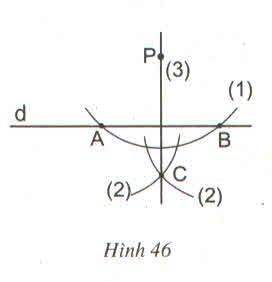
a) Ta có PA = PB (A, B nằm trên cung tròn có tâm P) CA = CB (hai cung tròn AB có tâm A và B có bán kính bằng nhau; C la giao điểm của 2 cung)
Vậy P; C cách đều A và B nên đường thẳng CP là đường trung trực của AB nên
PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.
=> PC ⊥ d (đpcm)
Hướng dẫn:
a) Ta có PA = PB (A, B nằm trên cung tròn có tâm P) CA = CB (hai cung tròn AB có tâm A và B có bán kính bằng nhau; C la giao điểm của 2 cung)
Vậy P; C cách đều A và B nên đường thẳng CP là đường trung trực của AB nên
PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.
=> PC ⊥ d (đpcm)
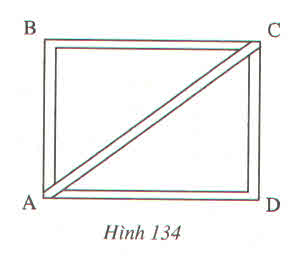
độ dài đường chéo AC là
\(\sqrt{48^2+36^2}=\sqrt{2304+1296}=\sqrt{3600}=60\)(cm)
vậy độ dài đường chéo AC là 60cm
Giải:
Theo định lí Pytago, ta có:
AC2= AD2 +CD2
= 482 + 362
= 2304 + 1296= 3600
AC= 60 (cm)
Hình ảnh của chiếc ***** ta thấy một cách trực quan các cặp góc so le trong cũng như các cặp góc đồng vị.
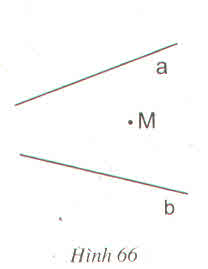
- Vẽ đường thẳng qua M vuông góc với a tại P cắt b tại Q.
- Vẽ đường thẳng qua M vuông góc với b tại R cắt a tại S.
- Vẽ đường thẳng qua M vuông góc với SQ.
=> Đây chính là đường qua M và qua giao điểm của hai đường a, b.
Áp dụng bài 69 ta có cách vẽ sau:
-Vẽ đường thẳng qua M vuông góc với a tại A cắt b tại B.
-Vẽ đường thẳng qua M vuông góc với b tại C cắt a tại D.
-Vẽ đường thẳng c qua M vuông góc với BD
=>C là đường qua M và qua giao điểm của hai đường a, b
Vì 3 đường thẳng a, b, c là 3 đường cao trong ∆DMB nên đồng quy