K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DC
1
8 tháng 11 2017
8 túi đựng số viên bi đỏ là:
8 . 9 = 72 (viên bi)
6 túi đựng số viên bi xanh là:
6 . 8 = 48 (viên bi)
Vì 72 ⋮ a và 48 ⋮ a nên a là ƯCLN của 72 và 48
72 = 23 . 33
48 = 24 . 3
ƯCLN(72;48) = 23 . 3 = 24
Vậy Bình có thể chia nhiều nhất số bi vào 24 hộp. Mỗi hộp có 3 viên bi đỏ, 2 viên bi xanh.
T
9 tháng 4 2022
Câu 14)
\(a,\\ =-\dfrac{3}{8}+\dfrac{8}{17}+\dfrac{-5}{8}-\dfrac{3}{5}+\dfrac{9}{17}\\ =\left(\dfrac{-3}{8}+\dfrac{-5}{8}\right)+\left(\dfrac{8}{17}+\dfrac{9}{17}\right)-\dfrac{3}{5}\\ =\left(-1\right)+1-\dfrac{3}{5}=0-\dfrac{3}{5}=\dfrac{-3}{5}\\ b,\\ =\dfrac{7}{15}.\dfrac{-15}{14}+\left(\dfrac{27}{16}-\dfrac{1}{8}\right):\dfrac{5}{8}\)
\(=\dfrac{-1}{2}+\dfrac{25}{16}.\dfrac{8}{5}=\dfrac{-1}{2}+\dfrac{5}{2}=2\\ c,\\ =\dfrac{2}{2}-\dfrac{2}{3}+\dfrac{2}{3}-\dfrac{2}{4}+.....+\dfrac{2}{99}-\dfrac{2}{100}\\ =1-\dfrac{1}{50}=\dfrac{49}{50}\)
Câu 15
\(a,2x+\dfrac{-1}{4}=\dfrac{3}{2}\\ 2x=\dfrac{3}{2}-\dfrac{-1}{4}=\dfrac{7}{4}\\ x=\dfrac{7}{4}:2=\dfrac{7}{8}\\ b,\dfrac{15}{x}=\dfrac{-3}{4}\\ x=\dfrac{15.4}{-3}=-20\)
K1
3
6 tháng 11 2017
\(a.\left(x+2\right)\cdot y=11\left(x+2>1\right)\)
\(\Rightarrow x+2;y\inƯ\left(11\right)=\left\{1;11\right\}\)
Mà vì x+2 > 1 Nên ta có
\(x+2=11\Rightarrow x=9;y=1\)
\(b.\left(x-1\right)\cdot\left(y-1\right)=15\)
\(\Rightarrow x-1;y-1\inƯ\left(15\right)=\left\{1;3;5;15\right\}\)
Ta có các đáp án sau :
\(x-1=1;y-1=15\Rightarrow x=2;y=16\)
\(x-1=15;y-1=1\Rightarrow x=16;y=2\)
\(x-1=3;y-1=5\Rightarrow x=4;y=6\)
\(x-1=5;y-1=3\Rightarrow x=6;y=4\)
YN
2
12 tháng 2 2020
\(M=\frac{1}{3^0}+\frac{1}{3^1}+\frac{1}{3^2}+...+\frac{1}{3^{2005}}\)
\(\frac{1}{3}\cdot M=\frac{1}{3}\cdot\left(\frac{1}{3^0}+\frac{1}{3^1}+\frac{1}{3^2}+...+\frac{1}{3^{2005}}\right)\)
\(\frac{1}{3}\cdot M=\frac{1}{3^1}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{2006}}\)
\(\frac{1}{3}\cdot M-M=-\frac{2}{3}\cdot M=\frac{1}{3^1}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{2006}}-\left(\frac{1}{3^0}+\frac{1}{3^1}+\frac{1}{3^2}+...+\frac{1}{3^{2005}}\right)\)
\(-\frac{2}{3}\cdot M=\frac{1}{3^1}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{2006}}-\frac{1}{3^0}-\frac{1}{3^1}-\frac{1}{3^2}-...-\frac{1}{3^{2005}}\)
\(-\frac{2}{3}\cdot M=\frac{1}{3^{2006}}-\frac{1}{3^0}=\frac{1}{3^{2006}}-\frac{1}{1}=\frac{1}{3^{2006}}-1\Rightarrow M=\left(\frac{1}{3^{2006}}-1\right):\left(-\frac{2}{3}\right)\)
\(M=\left(\frac{1}{3^{2006}}-1\right)\cdot\left(-\frac{3}{2}\right)=\frac{1}{3^{2006}}\cdot\left(-\frac{3}{2}\right)-\left(-\frac{3}{2}\right)=-\frac{3}{3^{2006}\cdot2}-\left(-\frac{3}{2}\right)\)
Chúc bạn học tốt ^^!!!
12 tháng 2 2020
\(M=\frac{1}{3^0}+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{2005}}\)
\(\Rightarrow3M=3+1+\frac{1}{3}+...+\frac{1}{3^{2004}}\)
\(\Rightarrow3M-M=\left(3+1+\frac{1}{3}+...+\frac{1}{3^{2004}}\right)-\left(\frac{1}{3^0}+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{2005}}\right)\)
\(\Rightarrow2M=3-\frac{1}{3^{2004}}\)
\(\Rightarrow M=\frac{3-\frac{1}{3^{2004}}}{2}\)
11 tháng 7 2017
Nếu là z+x thì mik biết làm nè:
Đặt x-y=2011(1)
y-z=-2012(2)
z+x=2013(3)
Cộng (1);(2);(3) lại với nhau ta được :
2x=2012=>x=1006
Từ (1) => y=-1005
Từ (3) => z=1007
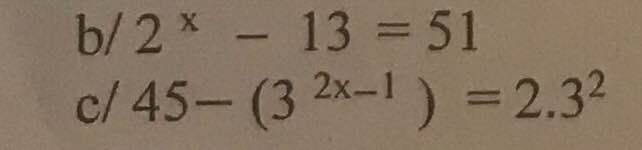
cj e kêu k dc giúp e kìa =))))
\(b,2^x=51+13=64\Rightarrow2^{x^{ }}=2^6\Rightarrow x=6\)
\(c,\left(3^{2x-1}\right)=45-18\\ \left(3^{2x-1}\right)=27\\ 3^{2x-1}=3^3\\ 2x-1=3\\ 2x=4\\ x=4:2\\ x=2\)