Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giả sử 4 nghiệm phân biệt của phương trình là : \(x_1;x_2;x_3;x_4\)
Đặt \(x^2=y\ge0\), ta có phương trình :
\(\Leftrightarrow y^2-\left(3m+5\right)y+\left(m+1\right)^2=0\left(1\right)\)
Ta phải tìm m sao cho (1) có hai nghiệm phân biệt \(0 < y1 < y2\)
Khi đó (1) có 4 nghiệm là : \(x_1=-\sqrt{y_2};x_2=-\sqrt{y_1};x_3=-\sqrt{y_1};x_4=-\sqrt{y_2}\)
Rõ ràng \(x2 < x2 < x3 < x4\)
Theo đầu bài thì bốn nghiệm lập thành cấp số cộng, nên :
\(\Rightarrow x_3+x_1=2x_2\) V \(x_4+x_1=2x_3\)
\(\Leftrightarrow\sqrt{y_1}-\sqrt{y_2}=2\sqrt{y_1}\)
\(\Rightarrow3\sqrt{y_1}=\sqrt{y_2}\)
\(\Leftrightarrow9y_1=y_2\) (*)
Áp dụng Viet cho phương trình (1) ta có hệ :
\(\begin{cases}\Delta=\left(3m+5\right)^2-4\left(m+1\right)^2>0\\S=y_1+y_2=10y_1=3m+5\\P=y_1y_2=9y_1^2=\left(m+1\right)^2\end{cases}\)
\(\Leftrightarrow\begin{cases}m=5\\m=-\frac{25}{19}\end{cases}\)
16.
\(y'=\frac{\left(cos2x\right)'}{2\sqrt{cos2x}}=\frac{-2sin2x}{2\sqrt{cos2x}}=-\frac{sin2x}{\sqrt{cos2x}}\)
17.
\(y'=4x^3-\frac{1}{x^2}-\frac{1}{2\sqrt{x}}\)
18.
\(y'=3x^2-2x\)
\(y'\left(-2\right)=16;y\left(-2\right)=-12\)
Pttt: \(y=16\left(x+2\right)-12\Leftrightarrow y=16x+20\)
19.
\(y'=-\frac{1}{x^2}=-x^{-2}\)
\(y''=2x^{-3}=\frac{2}{x^3}\)
20.
\(\left(cotx\right)'=-\frac{1}{sin^2x}\)
21.
\(y'=1+\frac{4}{x^2}=\frac{x^2+4}{x^2}\)
22.
\(lim\left(3^n\right)=+\infty\)
11.
\(\lim\limits_{x\rightarrow1^+}\frac{-2x+1}{x-1}=\frac{-1}{0}=-\infty\)
12.
\(y=cotx\Rightarrow y'=-\frac{1}{sin^2x}\)
13.
\(y'=2020\left(x^3-2x^2\right)^{2019}.\left(x^3-2x^2\right)'=2020\left(x^3-2x^2\right)^{2019}\left(3x^2-4x\right)\)
14.
\(y'=\frac{\left(4x^2+3x+1\right)'}{2\sqrt{4x^2+3x+1}}=\frac{8x+3}{2\sqrt{4x^2+3x+1}}\)
15.
\(y'=4\left(x-5\right)^3\)
3.
\(x-2y+1=0\Leftrightarrow y=\frac{1}{2}x+\frac{1}{2}\)
\(y'=\frac{2}{\left(x+1\right)^2}\Rightarrow\frac{2}{\left(x+1\right)^2}=\frac{1}{2}\)
\(\Rightarrow\left(x+1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=3\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=\frac{1}{2}\left(x-1\right)+1\\y=\frac{1}{2}\left(x+3\right)+3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=\frac{1}{2}x+\frac{1}{2}\left(l\right)\\y=\frac{1}{2}x+\frac{9}{2}\end{matrix}\right.\)
4.
\(\lim\limits\frac{\sqrt{2n^2+1}-3n}{n+2}=\lim\limits\frac{\sqrt{2+\frac{1}{n^2}}-3}{1+\frac{2}{n}}=\sqrt{2}-3\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
5.
\(\lim\limits_{x\rightarrow a}\frac{2\left(x^2-a^2\right)+a\left(a+1\right)-\left(a+1\right)x}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+2a\right)-\left(a+1\right)\left(x-a\right)}{\left(x-a\right)\left(x+a\right)}\)
\(=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+a-1\right)}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{2x+a-1}{x+a}=\frac{3a-1}{2a}\)
1.
\(f'\left(x\right)=-3x^2+6mx-12=3\left(-x^2+2mx-4\right)=3g\left(x\right)\)
Để \(f'\left(x\right)\le0\) \(\forall x\in R\) \(\Leftrightarrow g\left(x\right)\le0;\forall x\in R\)
\(\Leftrightarrow\Delta'=m^2-4\le0\Rightarrow-2\le m\le2\)
\(\Rightarrow m=\left\{-1;0;1;2\right\}\)
2.
\(f'\left(x\right)=\frac{m^2-20}{\left(2x+m\right)^2}\)
Để \(f'\left(x\right)< 0;\forall x\in\left(0;2\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-20< 0\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{20}< m< \sqrt{20}\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m=\left\{1;2;3;4\right\}\)
Vì 3 nghiệm phân biệt : \(x_1,x_2,x_3\) lập thàng cấp số cộng, nên ta có thể đặt :
\(x_1=x_0-d,x_2=x_0;x_3=x_0+d\left(d\ne0\right)\). Theo giả thiết ta có :
\(x^3+3x^2-\left(24+m\right)x-26-n=\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\)
\(=\left(x-x_0+d\right)\left(x-x_0\right)\left(x-x_0-d\right)\)
\(=x^3-3x_0x^2+\left(3x^2_0-d^2\right)x-x^3_0+x_0d^2\) với mọi x
Đồng nhất hệ số ở hai vế của phương trình ta có hệ :
\(\begin{cases}-3x_0=3\\3x_0^2-d^2=-\left(24+m\right)\\-x_0^3+x_0d^2=-26-n\end{cases}\) \(\Leftrightarrow\begin{cases}x_0=-1\\3-d^2=-24-m\\1-d^2=-26-n\end{cases}\) \(\Leftrightarrow\begin{cases}x_0=-1\\m=n\end{cases}\)
Vậy với m = n thì 3 nghiệm phân biệt của phương trình lập thành cấp số cộng
Cho e hỏi là vì sao khúc cuối có dấu bằng mà trên đề k có dấu bằng ạ?
Vì mình lấy giá trị nguyên bạn
Chính xác là \(-\frac{1}{4}< k< \frac{2020-\frac{\pi}{2}}{2\pi}\)
\(\Rightarrow-0,25< k< 321,243\) (1)
Nhưng k nguyên nên chỉ cần lấy khoảng ở số nguyên gần nhất, tức là \(0\le k\le321\)
Để pt đã cho vô nghiệm thì:
\(1^2+\left(m-1\right)^2< \left(\sqrt{5}\right)^2\)
\(\Leftrightarrow\left(m-1\right)^2< 4\)
\(\Rightarrow-2< m-1< 2\)
\(\Rightarrow-1< m< 3\)
2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)
Chọn B.
Đặt t = x2, t ≥ 0.
Phương trình trở thành: t2 – 2(m + 1)t + 2m + 1 = 0 (2)
Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi PT (2) có hai nghiệm dương phân biệt t2 > t1 > 0.
Khi đó PT(2) có bốn nghiệm là: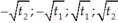
Bốn nghiệm này lập thành cấp số cộng khi :
Theo định lý viet thì :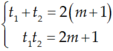
Vậy m = 4 hoặc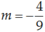
là những giá trị cần tìm.