Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vật đi qua vị trí cân bằng theo chiều dương :
\(\left\{{}\begin{matrix}x_0=0\\v_0>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A\cdot cos\varphi=0\\-\omega A\cdot sin\varphi>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=0\\sin\varphi< 0\end{matrix}\right.\)
\(\Leftrightarrow\varphi=\dfrac{-\pi}{2}\)
\(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
=> B

Chu kì: \(T=2.0,5=1s\)
Khoảng thời gian \(t=0,75s\Rightarrow \alpha =0,75.360=270^0\) = 3/4 vòng tròn.
Biểu diễn bằng véc tơ quay ta có:
Ban đầu, chất điểm ở vị trí M thì lúc sau sẽ đến N và có vị trí là -A

Đáp án B
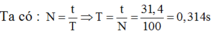
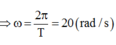
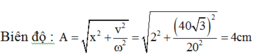
Tại thời điểm ban đầu t = 0 thì vật đang ở vị trí x = A 2 và đi theo chiều âm φ = π 3


Theo bài ra ta có
T = 10 π /100 = 0,1 π ⇒ ω = 2 π /T = 20rad/s
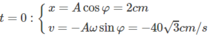
⇒ tan φ = 3 ⇒ φ = π /3; A = 4cm
⇒ x = 4cos(20t + π /3)

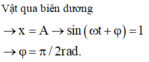
Đáp án A
Gốc thời gian lúc chất điểm đi qua vị trí cân bằng theo chiều dương