Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



bài 15 :
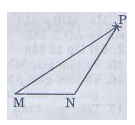
- Vẽ đoạn thẳng MN = 2,5cm.
- Trên cùng một nửa mặt phẳng bờ MN vẽ cung tròn tâm M bán kính 5cm, và cung tròn tâm N bán kính 3cm
- Hai cung tròn cắt nhau tại P. Vẽ các đoạn thẳng MP, NP ta được tam giác MNP.
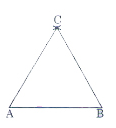
Vẽ tam giác ABC (tương tự với cách vẽ ở Bài 15):
- Vẽ cạnh AB có độ dài bằng 3 cm.
- Trên một nửa mặt phẳng bờ AB lần lượt vẽ hai cung tròn tại A và B có bán kính 3 cm
- Hai cung tròn này cắt nhau tại C. Nối các điểm A, B, C ta được tam giác ABC cần vẽ.
Đo mỗi góc của tam giác ABC ta được:

Ta có:
∆ MNQ = ∆ QPM (c.c.c)
vì MN = QP (gt)
NQ = PM(gt)
MQ = QM(cạnh chung)
MN=PQ ; MP = NQ ; hai tam giác có cạnh chung là MQ
=> \(\)MN // PQ
MP // NQ

Gọi số đo cạnh 1,cạnh 2,cạnh 3 lần lượt là:a,b,c(cm)(đk:a,b,c>0)
Vì cạnh 1,2,3 lần lượt tỉ lệ vs 2,3,4 nên:\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\)(1)
Vì chu vi tam giác là 45cm nên:a+b+c=45(2)
Từ (1) và (2). Áp dụng tính chất dãy tỉ số = nhau:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{45}{9}=5\)
Vậy \(\frac{a}{2}=5\)suy ra: a=2.5=10
\(\frac{b}{3}=5\)suy ra:a=3.5=15
\(\frac{c}{4}=5\)suy ra:c=4.5=20
Vậy cạh 1 là 10cm
cạnh 2 là 15cm
cạnh 3 là 20cm

Bài tập 1 SBT
a) Không đối đỉnh. Vì 1 cạnh của góc này không là tia đối của cạnh của góc kia
b) Đối đỉnh. Vì mỗi cạnh của góc này là tia đối của cạnh góc kia
c) Không đối đỉnh, vì không có đỉnh chung
d) Đối đỉnh, vì mỗi cạnh của góc này là tia đối của cạnh góc kia
e) Không đối đỉnh, vì không có cạnh nào của góc này là tia đối của 1 cạnh của góc kia
K mk nha, hứa sẽ k lại


Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của ΔABC và ΔA’B’C’ ta viết:
∆ABC= ∆A’B’C’.

∆ABC= ∆A’B’C’ nếu

Hướng dẫn giải bài tập SGK bài 2 tam giác bằng nhau trang 111, 112.
Bài 10. Trong các hình sau các Δ nào bằng nhau(Các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các Δ bằng nhau đó. Viết kí hiệu về sự bằng nhau của các Δ đó.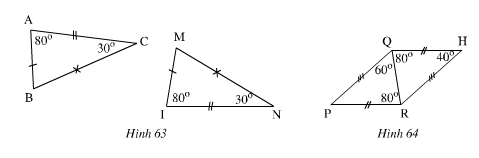
Hình 63:
Ta có:
- ∠A = ∠I = 800;
- ∠C = ∠N = 300
Xét ΔABC ta có: ∠B =1800 – (∠A+∠C)=1800 – (800+300) =700
Xét ΔMIN ta có: ∠M =1800 – (∠I+∠N)=1800 – (800+300) =700
- ⇒∠B = ∠M = 700
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC = ∆IMN
Hình 64:
Ta có:
∠RQH = ∠QRP = 800 (ở vị trí so le trong)
Nên QH // RP
Nên ∠HRQ = ∠PQR = 600(so le trong)
∠P = ∠H = 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR = ∆PRQ.
Bài 11. Cho ∆ ABC = ∆ HIK
a) Tìm cạnh tương ứng với cạnh BC. Tìm góc tương ứng với ∠H
b) Tìm các cạnh bằng nhau, tìm các góc bằng nhau.
HD: a) Ta có ∆ ABC = ∆ HIK, nên cạnh tương ứng với BC là cạnh IK. Góc tương ứng với ∠H là ∠A.
b) ∆ ABC= ∆ HIK
Suy ra: AB = HI, AC = HK, BC = IK.
∠A = ∠H, ∠B =∠I, ∠C = ∠K.
Luyện tập: Giải bài 12, 13, 14 trang 112 Toán 7 tập 1 (hình học)
Bài 12 trang 112. Cho ∆ ABC= ∆ HIK trong đó cạnh AB = 2cm. ∠B=400; BC= 4cm. Em có thể suy ra số đo của những cạnh nào, những góc nào của ΔHIK?
Ta có ∆ ABC= ∆ HIK (gt)
Suy ra: AB = HI= 2cm, BC = IK= 4cm, ∠I = ∠B = 400
Bài 13. Cho ∆ ABC= ∆ DEF. Tính chu vi mỗi tam giá nói trên biết AB = 4cm, BC = 6cm, DF = 5cm (chu vi của một tam giác là tổng độ dài ba cạnh của tam giác đó)
Ta có ∆ABC = ∆ DEF
Suy ra: AB = DE= 4cm, BC = EF = 6cm, DF = AC = 5cm.
Chu vi của ΔABC bằng: AB + BC + AC = 4 + 5 + 6 = 15 (cm)
Chu vi của ΔDEF bằng: DE + EF + DF = 4 + 5 + 6 = 15 (cm )
Bài 14 trang 112. Cho hai tam giác bằng nhau: ΔABC (Không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và một Δ có ba đỉnh H, I ,K. Viết kí hiệu về sự bằng nhau của hai Δ đó biết: AB=KI, ∠B =∠K.
Giải: Ta có: ∠B =∠K nên B, K là hai đỉnh tương ứng.
AB= KI nên A, I là hai đỉnh tương ứng.
Vậy ∆ABC = ∆IKH.
![]()

Hình a)
Áp dụng định lí Pytago, Ta có:
x2 =122+5 = 144+25=169
=> 132=x2 => x=13.
Hình b) ta có:
x2= 12 + 22 = 1+4=5
x= √5
Hình c)
Theo định lí pytago:
292=212+x2
nên x2=292-212
= 841-441=400=202
=>x=20
Hình d)
x2=( √7)2+32=7+9=16=42
=>x=4.
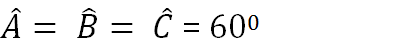

Hai tam giác ADE và OCB có:
OB = AD = r
BC = DE ( giả thiết )
OC = AE = r
\(\Rightarrow\Delta ADE=\Delta OBC\) (c.c.c)
Vậy \(\widehat{DAE}=\widehat{xOy}\) ( góc tương ứng) (đpcm)
Hai tam giác ACB và ADB có:
AC = AD = 2 cm
BC = BD = 3 cm
AB cạnh chung
\(\Rightarrow\Delta ACB=\Delta ADB\) (c.c.c)
\(\Rightarrow\widehat{CAB}=\widehat{DAB}\) ( góc tương ứng )
Vậy AB là tia phân giác của góc CAD
bài 22
Tam giác DAE và BOC có:
AD=OB(gt)
DE=BC(gt)
AE=OC(gt)
Nên ∆ DAE= ∆ BOC(c.c.c)
suy ra ˆDAEDAE^=ˆBOCBOC^(hai góc tương tứng)
vậy
ˆDAE=ˆxOy.DAE^=xOy^.
bài 23
Vì CC là giao của đường tròn tâm AA và tâm BB nên AC=2cm,BC=3cmAC=2cm,BC=3cm
Vì DD là giao của đường tròn tâm AA và tâm BB nên AD=2cm,BD=3cmAD=2cm,BD=3cm
Do đó AC=AD,BC=BDAC=AD,BC=BD
Xét ΔBAC∆BAC và ΔBAD∆BAD có:
+) AC=ADAC=AD
+) BC=BDBC=BD
+) ABAB cạnh chung.
Suy ra ΔBAC=ΔBAD(c.c.c)∆BAC=∆BAD(c.c.c)
Suy ra ˆBACBAC^ = ˆBADBAD^ (hai góc tương ứng)
Vậy ABAB là tia phân giác của góc CADCAD.