Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vận dụng định lý về tỉ số lượng giác của hai góc phụ nhau ta có:
sin60° = cos(90° – 60°) = cos30°
Tương tự:
cos75° = sin(90° – 75°) = sin 15°
sin52°30′ = cos(90° – 52°30′) = 38°30′
cotg82° = tg8°; tg80° = cotg10°

Vẽ tam giác ABC vuông tại A, góc C = 34°

Theo định nghĩa ta có:

Hướng dẫn giải:
Vẽ tam giác ABC vuông tại A, ˆC=34∘C^=34∘
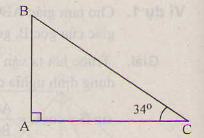
Theo định nghĩa ta có:
sin34∘=ABBCsin34∘=ABBC
cos34∘=ACBCcos34∘=ACBC
tg34∘=ABACtg34∘=ABAC
cotg34∘=ACABcotg34∘=ACAB.

\(\sin60^o=\cos30^o\)
\(\cos75^o=\sin15^o\)
\(\cot82^o=\tan8^o\)
\(\tan80^o=\cot10^o\)
\(\sin52^o3'=\cos37^o57'\)
\(sin60=cos\left(90^0-60^0\right)=cos30^0\)
\(cos75^0=sin\left(90^0-75^0\right)=sin15^0\)
\(cot82^0=tan\left(90^0-82^0\right)=tan8^0\)
\(tan80^0=cot\left(90^0-80^0\right)=cot10^0\)
\(sin52^03'=cos\left(90^0-52^03'\right)=cos37^057'\)

a) cos14∘=sin76∘;cos87∘=sin3∘.cos14∘=sin76∘;cos87∘=sin3∘..
Vì sin3∘<sin47∘<sin76∘<sin78∘sin3∘<sin47∘<sin76∘<sin78∘ nên
cos78∘<cos76∘<cos47∘<cos3∘cos78∘<cos76∘<cos47∘<cos3∘.
b) cotg25∘=tg65∘;cotg38∘=tg52∘cotg25∘=tg65∘;cotg38∘=tg52∘.
Vì tg52∘<tg62∘<tg65∘<tg73∘tg52∘<tg62∘<tg65∘<tg73∘;
nên cotg38∘<tg62∘<cotg25∘<tg73∘cotg38∘<tg62∘<cotg25∘<tg73∘.
Nhận xét: Để so sánh các tỉ số lượng giác sin và côsin của các góc, ta đưa về so sánh cùng một loại tỉ số lượng giác (ví dụ cùng là sin của các góc). Tương tự như vậy, để so sánh các tỉ số lượng giác tang và côtang của các góc, ta đưa về so sánh cùng một loại tỉ số lượng giác (ví dụ cùng là tang của các góc).
a) cos14∘=sin76∘;cos87∘=sin3∘..
Vì sin3∘<sin47∘<sin76∘<sin78∘ nên
cos78∘<cos76∘<cos47∘<cos3∘.
b) cotg25∘=tg65∘;cotg38∘=tg52∘.
Vì tg52∘<tg62∘<tg65∘<tg73∘;
nên cotg38∘<tg62∘<cotg25∘<tg73∘.
Nhận xét: Để so sánh các tỉ số lượng giác sin và côsin của các góc, ta đưa về so sánh cùng một loại tỉ số lượng giác (ví dụ cùng là sin của các góc). Tương tự như vậy, để so sánh các tỉ số lượng giác tang và côtang của các góc, ta đưa về so sánh cùng một loại tỉ số lượng giác (ví dụ cùng là tang của các góc).

Các tỉ số lượng giác góc \(\alpha\)là:
\(\sin40^0\approx0,6428\)
\(\cos40^0\approx0,7660\)
\(\tan40^0\approx0,8391\)
\(\cot40^0\approx1,1918\)


sin60o = cos30o
cos75o = sin15o
sin50o30' = cos39o30'
cot82o = tan8o
tan78o = cot12o