Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một hàm số cho bởi công thức y = f(x) mà không chú thích gì về tập các định thì ta quy ước rằng tập xác định của hàm số ấy là tập hợp tất cả x ∈ R sao cho biểu thức f(x) có nghĩa.
Hàm số \(y=\dfrac{x+1}{\left(x+1\right)\left(x^2+2\right)}\) có tập xác định là D = R/{-1}, còn hàm số \(y=\dfrac{1}{x^2+2}\). Do đó hai hàm số khác nhau (mặc dù rằng với mọi x ≠ -1 giá trị của hàm số luôn bằng nhau khi x lấy cùng một giá trị.

Ví dụ hàm số $y=\frac{-1}{2}x$
Ta có bảng sau:

Với mỗi giá trị của x ta có 1 giá trị của y, vậy bảng trên biểu thị cho 1 hàm số
Tập xác định của hàm số \(D = \left\{ { - 2; - 1; - \frac{1}{2};0;\frac{1}{2};1;2} \right\}\)
Tập giá trị của hàm số \(\left\{ {1;\frac{1}{2};\frac{1}{4};0; - \frac{1}{4}; - \frac{1}{2}; - 1} \right\}\)

Đáp án A
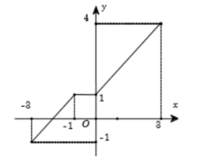
Trên khoảng (−3; −1) và (1; 3) đồ thị hàm số đi lên từ trái sang phải
=> Hàm số đồng biến trên khoảng (−3; −1) và (1; 3).

Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D

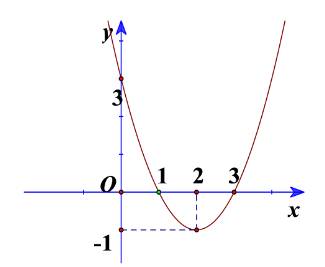
a) Trục đối xứng là đường thẳng \(x = 2\)
Đỉnh là \(I\left( {2; - 1} \right)\)
b) Từ đồ thị ta thấy trên khoảng \(\left( { - \infty ;2} \right)\) thì hàm số đi xuống nên hàm số nghịch biến trên \(\left( { - \infty ;2} \right)\).
Trên khoảng \(\left( {2; + \infty } \right)\) thì hàm số đi xuống nên đồng biến trên \(\left( {2; + \infty } \right)\).
c) ) Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Đồ thị hàm số có đỉnh là \(I\left( {2; - 1} \right)\) nên ta có:
\(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\a{.2^2} + b.2 + c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2b + c = - 1\end{array} \right.\)
Ta lại có điểm \(\left( {1;0} \right)\) thuộc đồ thị nên ta có: \(a + b + c = 0\)
Vậy ta có hệ sau:
\(\left\{ \begin{array}{l}b = - 4a\\4a + 2b + c = - 1\\a + b + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2.\left( { - 4a} \right) + c = - 1\\a + \left( { - 4a} \right) + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\c - 4a = - 1\\c - 3a = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\a = 1\\c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4\\a = 1\\c = 3\end{array} \right.\)
Vậy parabol là \(y = {x^2} - 4x + 3\)

a) Mỗi giá trị của x tương ứng sẽ có 1 giá trị của y nên Bảng 6.4 cho ta một hàm số.
Tập xác định của hàm số \(D = \left\{ {2013;2014;2015;2016;2017;2018} \right\}\)
Tập giá trị của hàm số \(\left\{ {73,1;73,2;73,3;73,4;73,5} \right\}\)
b) Giá trị của hàm số tại x=2018 là 242
Tập xác định của hàm số \(D = \left( {2013;2019} \right)\)
Tập giá trị của hàm số \(\left( {236;242} \right)\)
c)\(\)\(\begin{array}{l}f(1) = - {2.1^2} = - 2\\f(2) = - {2.2^2} = - 8\end{array}\)
Tập xác định của hàm số \(y = f(x) = - 2{x^2}\)là \(\mathbb{R}\)
Ta có \({x^2} \ge 0 \Rightarrow - 2{x^2} \le 0\) , do đó \(y \le 0\)
Tập giá trị của hàm số \(y = f(x) = - 2{x^2}\) là \(\left( { - \infty ;0} \right)\)

ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)

Từ bảng giá trị vận tốc v (mét/giây) ở thời điểm t (giây) của vật chuyển động, ta thấy ứng với mỗi thời điểm t (giây) trong bảng đều có một giá trị vận tốc v duy nhất. Vì vậy, bảng này biểu thị một hàm số.
Hàm số đó có tập xác định \(D = \{ 0,5;1;1,2;1,8;2,5\} \)
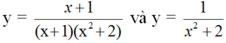
- Tập xác định của hàm số cho bởi công thức y = f(x) là tập hợp các giá trị của x sao cho biểu thức f(x) có nghĩa.
- Với quy ước đó:
Vậy tập xác định của hàm số là D = R
Kết luận: Hai hàm số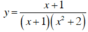 và
và 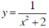 có tập xác định khác nhau.
có tập xác định khác nhau.