Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Mỗi giá trị của x tương ứng sẽ có 1 giá trị của y nên Bảng 6.4 cho ta một hàm số.
Tập xác định của hàm số \(D = \left\{ {2013;2014;2015;2016;2017;2018} \right\}\)
Tập giá trị của hàm số \(\left\{ {73,1;73,2;73,3;73,4;73,5} \right\}\)
b) Giá trị của hàm số tại x=2018 là 242
Tập xác định của hàm số \(D = \left( {2013;2019} \right)\)
Tập giá trị của hàm số \(\left( {236;242} \right)\)
c)\(\)\(\begin{array}{l}f(1) = - {2.1^2} = - 2\\f(2) = - {2.2^2} = - 8\end{array}\)
Tập xác định của hàm số \(y = f(x) = - 2{x^2}\)là \(\mathbb{R}\)
Ta có \({x^2} \ge 0 \Rightarrow - 2{x^2} \le 0\) , do đó \(y \le 0\)
Tập giá trị của hàm số \(y = f(x) = - 2{x^2}\) là \(\left( { - \infty ;0} \right)\)

Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)

- Tập xác định của hàm số cho bởi công thức y = f(x) là tập hợp các giá trị của x sao cho biểu thức f(x) có nghĩa.
- Với quy ước đó:
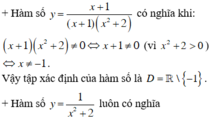
Vậy tập xác định của hàm số là D = R
Kết luận: Hai hàm số 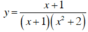 và
và 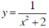 có tập xác định khác nhau.
có tập xác định khác nhau.

a) Ta có \((x - 1)(2 - 3x) = 2x - 3{x^2} - 2 + 3x = - 3{x^2} + 5x - 2\)
Do đó hàm y=(x-1)(2-3x) là hàm số bậc hai với \(a = - 3;b = 5;c = - 2\)
b) Thay các giá trị của x vào y = (x - 1)(2 - 3x) ta có:


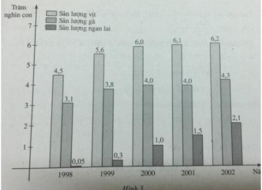
Tập xác định của cả ba hàm số y = f(x), y = g(x) và y = h(x) là:
D = {1998, 1999, 2000, 2001, 2002}

Từ đồ thị, ta có:
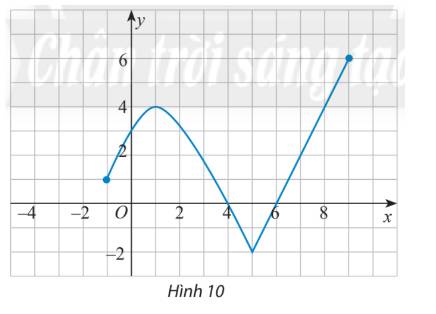
Đồ thị hàm số xác định (liền mạch) từ \(x = - 1\) đến \(x = 9\), do đó tập xác định của hàm số là \(D = [ - 1;9].\)
Tập giá trị \(T = \{ y|x \in [ - 1;9]\} \), vậy \(T = [ - 2;6]\)

Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
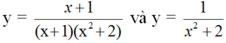
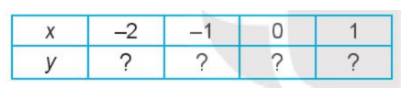
Ví dụ hàm số $y=\frac{-1}{2}x$
Ta có bảng sau:
Với mỗi giá trị của x ta có 1 giá trị của y, vậy bảng trên biểu thị cho 1 hàm số
Tập xác định của hàm số \(D = \left\{ { - 2; - 1; - \frac{1}{2};0;\frac{1}{2};1;2} \right\}\)
Tập giá trị của hàm số \(\left\{ {1;\frac{1}{2};\frac{1}{4};0; - \frac{1}{4}; - \frac{1}{2}; - 1} \right\}\)