Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xy(x+y)+yz(y+z)+xz(x+z)+2xyz
= xy(x + y) + yz(y + z) + xyz + xz(x + z) + xyz
= xy(x + y) + yz(y + z + x) + xz(x + z + y)
= xy(x + y) + z(x + y + z)(y + x)
= (x + y)(xy + zx + zy + z²)
= (x + y)[x(y + z) + z(y + z)]
= (x + y)(y + z)(z + x)
.
.
.
xy(x+y)+yz(y+z)+xz(x+z)+2xyz
= xy(x + y) + yz(y + z) + xyz + xz(x + z) + xyz
= xy(x + y) + yz(y + z + x) + xz(x + z + y)
= xy(x + y) + z(x + y + z)(y + x)
= (x + y)(xy + zx + zy + z²)
= (x + y)[x(y + z) + z(y + z)]
= (x + y)(y + z)(z + x)

\(xy\left(x-y\right)+yz\left(y-z\right)+xz\left(z-x\right)\)
\(=xy\left(x-y\right)+yz\left[\left(y-x\right)-\left(z-x\right)\right]+xz\left(z-x\right)\)
\(=xy\left(x-y\right)-yz\left(x-y\right)-yz\left(z-x\right)+xz\left(z-x\right)\)
\(=\left(x-y\right)\left(xy-yz\right)-\left(z-x\right)\left(yz-xz\right)\)
\(=\left(x-y\right)\left(xy-yz\right)+\left(z-x\right)\left(xz-yz\right)\)
\(=\left(xy-yz\right)\left(x-y+z-x\right)\)
\(=\left(xy-yz\right)\left(-y+z\right)\)
mơn bn nha ^^
nh sáng nay lên lp thầy chữa bài thì kq nó k như z, cả cách lm nx :v
kq là: ( z - y )( x - z)( y - x )


xy(x-y)+yz(y-z)+xz(x-z)
=y.[x.(x-y)+z.(y-z)]+xz(x-z)
=y.(x2-xy+zy-z2)+xz.(x-z)
=y.[(x2-z2)+(-xy+zy)]+xz.(x-z)
=y.[(x-z)(x+z)-y.(x-z)]+xz.(x-z)
=y.(x-z)(x+z-y)+xz.(x-z)
=(x-z)[y.(x+z-y)+xz]
=(x-z)(xy+yz-y2+xz)

xy(x+y)+yz(y+z)+xz(x+z)+2xyz
= xy(x + y) + yz(y + z) + xyz + xz(x + z) + xyz
= xy(x + y) + yz(y + z + x) + xz(x + z + y)
= xy(x + y) + z(x + y + z)(y + x)
= (x + y)(xy + zx + zy + z2)
= (x + y)[x(y + z) + z(y + z)]
= (x + y)(y + z)(z + x)
xy(x+y)+yz(y+z)+xz(x+z)+2xyz
= xy(x + y) + yz(y + z) + xyz + xz(x + z) + xyz
= xy(x + y) + yz(y + z + x) + xz(x + z + y)
= xy(x + y) + z(x + y + z)(y + x)
= (x + y)(xy + zx + zy + z²)
= (x + y)[x(y + z) + z(y + z)]
= (x + y)(y + z)(z + x)

tao có \(xz\left(z-x\right)+yz\left(y+z\right)-xy\left(x+y\right)=xz\left(z-x\right)+yz\left(y+x+z-x\right)-xy\left(x+y\right)=xz\left(z-x\right)+yz\left(z-x\right)+yz\left(x+y\right)-xy\left(x+y\right)\)
\(\left(z-x\right)\left(xz+yz\right)+\left(x+y\right)\left(yz-xy\right)=\left(z-x\right)z\left(x+y\right)+\left(x+y\right)y\left(z-x\right)=\left(z-x\right)\left(x+y\right)\left(z+y\right)\)
nếu mình giải khó hiểu thì cho mình xin lỗi nhé
\(xz\left(z-x\right)+yz\left(y+z\right)-xy+\left(x+y\right)\)
\(=xz^2-x^2z+yx\left(y+z\right)-xy\left(x+y\right)\)
\(=xz^2-x^2z+zy^2+z^2y-xy\left(x+y\right)\)
\(=xz^2-x^2z+zy^2+z^2y-x^2y-xy^2\)
P/s: ko chắc

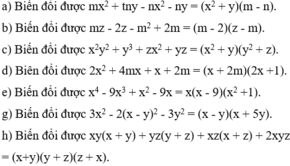
a, \(xy\left(x+y\right)+yz\left(y+z\right)+xz\left(x+z\right)+2xyz\)\(=x^2y+xy^2+y^2z+yz^2+x^2z+xz^2+2xyz\)
\(=\left(x^2y+xy^2+xyz\right)+\left(x^2z+xz^2+xyz\right)+\left(y^2z+yz^2\right)\)
\(=xy\left(x+y+z\right)+xz\left(x+z+y\right)+yz\left(y+z\right)\)
\(=x\left(x+y+z\right)\left(y+z\right)+yz\left(y+z\right)\)
\(=\left(y+z\right)\left(x^2+xy+xz+yz\right)\)
\(=\left(y+z\right)\left[x\left(x+z\right)+y\left(x+z\right)\right]\)
\(=\left(y+z\right)\left(x+z\right)\left(x+y\right)\)
b, \(2x^2+2y^2-x^2z+z-y^2z-2\)
\(=\left(2x^2-x^2z\right)+\left(2y^2-y^2z\right)-\left(2-z\right)\)
\(=x^2\left(2-z\right)+y^2\left(2-z\right)-\left(2-z\right)\)
\(=\left(2-z\right)\left(x^2+y^2-1\right)\)