Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A = 4acx + 4bcx + 4ax + 4bx ( đã sửa '-' )
= 4x( ac + bc + a + b )
= 4x[ c( a + b ) + ( a + b ) ]
= 4x( a + b )( c + 1 )
B = ax - bx + cx - 3a + 3b - 3c
= x( a - b + c ) - 3( a - b + c )
= ( a - b + c )( x - 3 )
C = 2ax - bx + 3cx - 2a + b - 3c
= x( 2a - b + 3c ) - ( 2a - b + 3c )
= ( 2a - b + 3c )( x - 1 )
D = ax - bx - 2cx - 2a + 2b + 4c
= x( a - b - 2c ) - 2( a - b - 2c )
= ( a - b - 2c )( x - 2 )
E = 3ax2 + 3bx2 + ax + bx + 5a + 5b
= 3x2( a + b ) + x( a + b ) + 5( a + b )
= ( a + b )( 3x2 + x + 5 )
F = ax2 - bx2 - 2ax + 2bx - 3a + 3b
= x2( a - b ) - 2x( a - b ) - 3( a - b )
= ( a - b )( x2 - 2x - 3 )
= ( a - b )( x2 + x - 3x - 3 )
= ( a - b )[ x( x + 1 ) - 3( x + 1 ) ]
= ( a - b )( x + 1 )( x - 3 )

a) \(2a^2x-5by-5a^2y+2by\)
\(=3\left(\frac{2}{3}a^2x-\frac{5}{3}a^2y\right)-3by\)
\(=3\left(\frac{2}{3}a^2x-\frac{5}{3}a^2y-by\right)\)

a) \(a^2+b^2+2ab+2a+2b+1=\left(a^2+2ab+b^2\right)+\left(2a+2b\right)+1\)
\(=\left(a+b\right)^2+2\left(a+b\right)+1=\left[\left(a+b\right)+1\right]^2=\left(a+b+1\right)^2\)
b) K phân tích dc.

\(2ax-bx+3cx-2a+b-3c\\ =x\left(2a-b+3c\right)-\left(2a-b+3c\right)\\ =\left(x-1\right)\left(2a-b+3c\right)\)
\(ax-bx-2cx-2a+2b+4c\\ =x\left(a-b-2c\right)-2\left(a-b-2c\right)\\ =\left(x-2\right)\left(a-b-2c\right)\)
\(3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\)
\(ax^2-bx^2-2ax+2bx-3a+3b\\ =x^2\left(a-b\right)-2x\left(a-b\right)-3\left(a+b\right)\\ =\left(x^2-2x-3\right)\left(a+b\right)\\ =\left(x+1\right)\left(x-3\right)\left(a+b\right)\)

Bài 2:
a) x(x - 3)- y(3 - x)
= x(x - 3) + y(x - 3)
= (x - 3)(x + y) (1)
Thay x = \(\frac{1}{3}\); y = \(\frac{8}{3}\)vào (1)
Ta có: (\(\frac{1}{3}\)- 3)(\(\frac{1}{3}\)+ \(\frac{8}{3}\))
= \(\frac{-8}{3}\). 3
= -8

Lời giải:
31.
\(2a^2x-5by-6a^2y+2bx=(2a^2x+2bx)-(5by+5a^2y)\)
\(=2x(a^2+b)-5y(b+a^2)=(a^2+b)(2x-5y)\)
34.
\(4acx+4bcx+4ax+4bx=4x(ac+bc+a+b)\)
\(=4x[(ac+bc)+(a+b)]=4x[c(a+b)+(a+b)]=4x(c+1)(a+b)\)
37. Sửa đề:
\(2ax^2-bx^2-2ax+bx+4a-2b\)
\(=(2ax^2-bx^2)-(2ax-bx)+(4a-2b)\)
\(=x^2(2a-b)-x(2a-b)+2(2a-b)=(2a-b)(x^2-x+2)\)
Câu 31:
\(2a^2x-5by-5a^2y+2bx\)
\(=2x\left(a^2+b\right)-5y\left(a^2+b\right)\)
\(=\left(a^2+b\right)\left(2x-5y\right)\)
Câu 34:
\(4acx+4bcx+4ax+4bx\)
\(=4cx\left(a+b\right)+4x\left(a+b\right)\)
\(=\left(a+b\right)\left(4cx+4x\right)\)
\(=4x\left(a+b\right)\left(c+1\right)\)
Câu 37:
\(2ax^2-bx^2-2ax+bx+4a-2b\)
\(=x^2\left(2a-b\right)-x\left(2a-b\right)+2\left(2x-b\right)\)
\(=\left(2a-b\right)\left(x^2-x+2\right)\)
\(=\left(2a-b\right)\left(x^2-x+2\right)\)
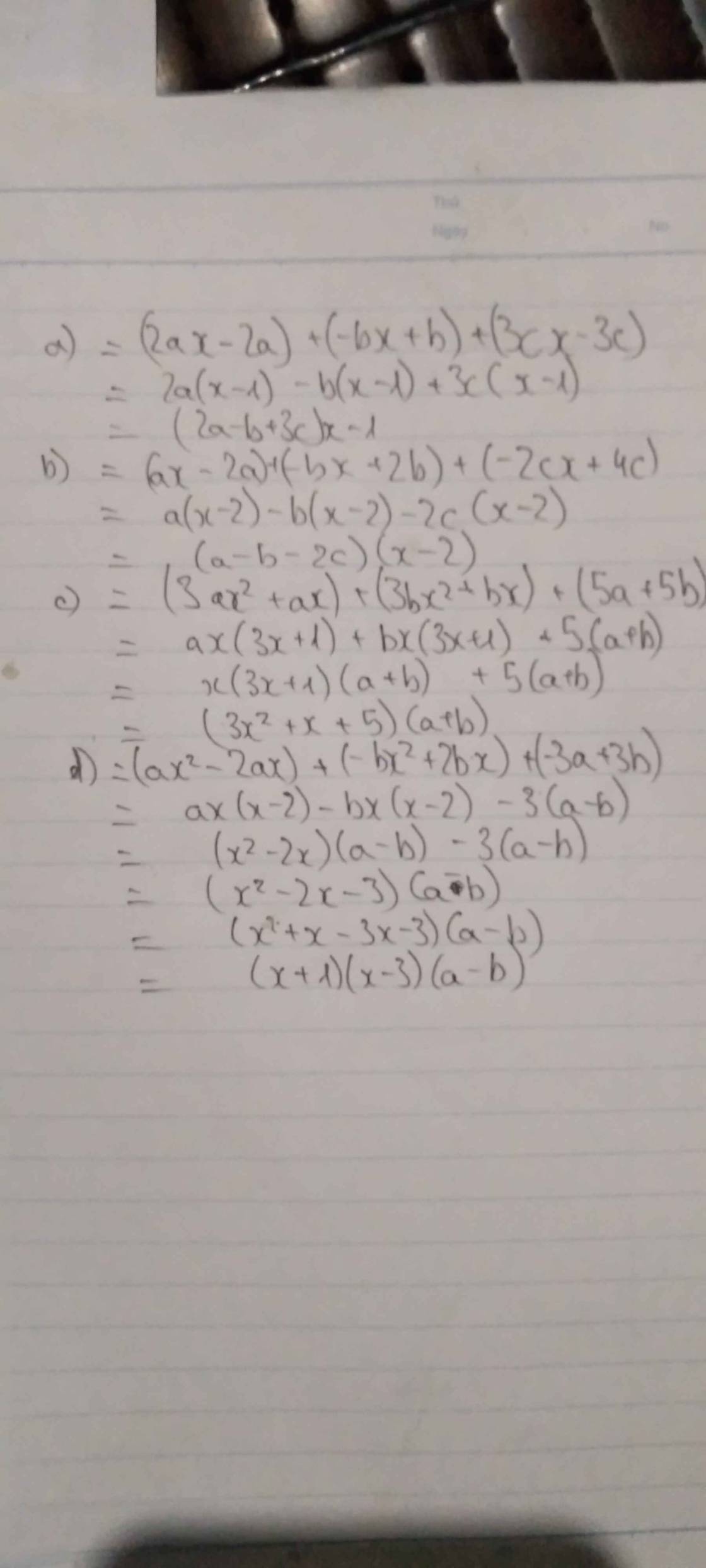
a, x(a - b) + (a - b)
= (x + 1)(a - b)
b, x(a + b) - a - b
= x(a + b) - (a + b)
= (x - 1)(a + b)
c, 10ax - 5ay - 2x + y
= 5a(2x - y) - (2x - y)
= (5a - 1)(2x - y)
d, 2a^2x - 5by - 5a^2y + 2bx
= 2x(a^2 + b) - 5y(b + a^2)
= (2a - 5y)(a^2 + b)
làm tiếp:
2ax2 - bx2 - 2ax +bx +4a-2b
= x2(2a-b) - x(2a-b) +2(2a-b)
=(2a-b)(x2-x+2)