Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)

a: \(A=\left\{0;1;2;3;4;5\right\}\)
b: \(B=\left\{2;3;4;5\right\}\)
c: \(C=\left\{0;1;-1;2;-2;3;-3\right\}\)

Chọn A.
Ta có:
+) - x 2 + x - 1 = 0: PT vô nghiệm
+) 6 x 2 - 5x + 1 = 0
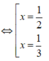
Lập bảng xét dấu:
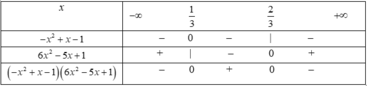
Suy ra
(- x 2 + x - 1)(6 x 2 - 5x + 1) > 0
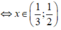
(- x 2 + x - 1)(6 x 2 - 5x + 1) < 0
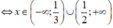

Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4

a)(x2-5x+6)(x2-5x+2)-5
Đặt \(x^2-5x+2=t\) ta được:
\(\left(t+4\right)t-16\)\(=t^2+4t-5\)
\(=t^2+5t-t-5\)
\(=t\left(t+5\right)-\left(t+5\right)\)
\(=\left(t-1\right)\left(t+5\right)\)\(=\left(x^2-5x+2-1\right)\left(x^2-5x+2+5\right)\)
\(=\left(x^2-5x+1\right)\left(x^2-5x+7\right)\)
b) (x2+8x-5)(x2+8x+1)-16
Đặt \(t=x^2+8x-5\) ta đc:
\(t\left(t+6\right)-16\)\(=t^2+6t-16\)
\(=t^2+8t-2t-16\)
\(=t\left(t+8\right)-2\left(t+8\right)\)
\(=\left(t-2\right)\left(t+8\right)\)\(=\left(x^2+8x-5-2\right)\left(x^2+8x-5+8\right)\)
\(=\left(x^2+8x-7\right)\left(x^2+8x+3\right)\)