
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Các phân số tối giản vì tử số và mẫu số của chúng không cùng chia hết cho số hơn lơn 1 ( hoặc vì ta không thể rút gọn được các phân số đó nữa):
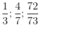
b) Phân số rút gọn :



\(\dfrac{9}{11}\) = \(\dfrac{36}{44}\)⇒ tỉ số tử số lúc đầu so với mẫu số lúc đầu là: \(\dfrac{36}{44}\)
\(\dfrac{5}{4}\) = \(\dfrac{55}{44}\) ⇒ tỉ số tử số lúc sau so với mẫu số lúc đầu là: \(\dfrac{55}{44}\)
Tỉ số của tử số lúc đầu so với tử số lúc sau là : \(\dfrac{36}{44}\) : \(\dfrac{55}{44}\) = \(\dfrac{36}{55}\)
Hiệu tử số lúc sau và tử số lúc đầu là 38
Tử số lúc đầu là: 38 : ( 55 - 36) \(\times\) 36 = 72
Mẫu số lúc đầu là: 72 : \(\dfrac{9}{11}\) = 88
Phân số cần tìm là \(\dfrac{72}{88}\)
Thử lại ta có \(\dfrac{72}{88}\) = \(\dfrac{9}{11}\) ( ok)
\(\dfrac{72+38}{88}\)= \(\dfrac{5}{4}\) ( ok nốt nhá em)
Vậy phân số \(\dfrac{72}{88}\) là phân số cần tìm

17/13= 17/13 , 14/23= 14/23 , 75/100=3/4 , 9/13=9/13 , 9/23=9/23 , 15/60=5/12

a) Các phân số tối giản vì tử số và mẫu số của chúng không cùng chia hết cho số hơn lơn 1 ( hoặc vì ta không thể rút gọn được các phân số đó nữa):
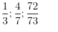
b) Phân số rút gọn :

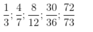
\(\frac{39}{65}=\frac{3}{5}\)
~~~Hok tốt~~~